Variations des fonctions
Fondamental : Théorème
Soit 
une fonction dérivable sur un intervalle 
inclus dans 
.
Si
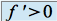sur , sauf peut-être en un nombre fini de points où elle s'annule, alors est strictement croissante sur ;Si
sur , sauf peut-être en un nombre fini de points où elle s'annule, alors est strictement décroissante sur ;Si
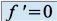sur , alors est constante sur .
L'étude des variations d'une fonction dérivable est donc la recherche des intervalles sur lesquels la dérivée garde un signe constant (on dit que sur ces intervalles, la fonction est monotone).
