Dérivabilité et continuité
Fondamental : Théorème
Si 
est dérivable en 
(ou à gauche de , ou à droite de ) alors est continue (ou à gauche de , ou à droite de ).
ATTENTION : la réciproque de ce théorème est fausse.
Exemple :
Soit la fonction définie sur 
par :
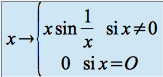
est continue en 0, en effet 
Pourtant n'est pas dérivable en 0, en effet
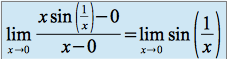
et 
n'existe pas.
