Dérivée d'une fonction composée
Fondamental : Théorème
Soit ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() contenant
contenant ![]() et
et ![]() une fonction définie sur un intervalle
une fonction définie sur un intervalle ![]() contenant
contenant ![]() . Si
. Si ![]() est dérivable en
est dérivable en ![]() et
et ![]() est dérivable en
est dérivable en ![]() alors la fonction
alors la fonction ![]() est dérivable en
est dérivable en ![]() et :
et : ![]() .
.
Si ![]() est dérivable sur
est dérivable sur ![]() , si
, si ![]() est dérivable sur
est dérivable sur ![]() et si pour tout
et si pour tout ![]() de
de ![]() ,
, ![]() appartient à
appartient à ![]() , alors
, alors ![]() est dérivable sur
est dérivable sur ![]() , et pour tout
, et pour tout ![]() ,
, ![]() .
.
On note
![]()
Démonstration : en supposant que si ![]() on a
on a ![]() , on peut alors écrire :
, on peut alors écrire :
![]() étant dérivable en
étant dérivable en ![]() , on obtient :
, on obtient :
![]()
de plus, ![]() étant dérivable en
étant dérivable en ![]() ,
, ![]() est continue en
est continue en ![]() , donc :
, donc :
![]()
et donc
![]()
Finalement :
![]()
Fondamental : Théorème
En particulier, ![]() est une fonction dérivable sur
est une fonction dérivable sur ![]() , les fonctions suivantes sont dérivables sur
, les fonctions suivantes sont dérivables sur ![]()
Pour
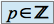 , si
, si 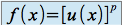 , alors
, alors 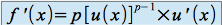 . (avec
. (avec 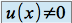 sur
sur  lorsque
lorsque 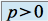 )
)Pour
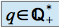 , si
, si 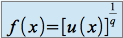 , alors
, alors 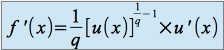 . (avec
. (avec 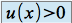 sur
sur  )
) Si
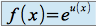 alors
alors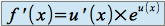 .
.Si
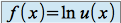 alors
alors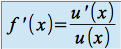 , avec
, avec 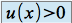 sur
sur  .
.
Exemple :
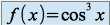 ,
,  est dérivable sur
est dérivable sur  et on a :
et on a :
 ,
,  est dérivable sur
est dérivable sur  et on a :
et on a :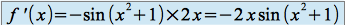
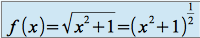 ,
,  est dérivable sur
est dérivable sur  et on a :
et on a :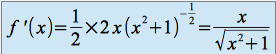
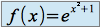 ,
,  est dérivable sur
est dérivable sur  et on a :
et on a :