Suites de Cauchy
Définition :
On dit qu'une suite numérique est de Cauchy si et seulement si :
Fondamental : Théorème
Soit 
une suite numérique réelle ou complexe, les propositions suivantes sont équivalentes
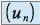- est une suite de Cauchy
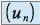- est convergente
