Comportement des suites monotones
Fondamental : Théorème (dit de la convergence monotone)
Toute suite croissante et majorée est convergente
Toute suite décroissante et minorée est convergente
Exemple :
Soit la suite 
définie de la façon suivante :
est le nombre obtenu en juxtaposant successivement tous les entiers 
après la virgule.
Il est facile de montrer que est croissante et majorée par 1. Donc converge.
Fondamental : Théorème
Toute suite croissante et non majorée tend vers
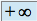
Toute suite décroissante et non minorée tend vers
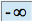
On en déduit :
Fondamental : Théorème
est un réel.
Si
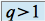, on a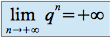 
Si
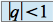, on a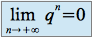 
Note : si 
, on a 
et donc 
Remarque :
Si 
, 
n'a pas de limite. prend des valeurs infiniment grandes en valeur absolue, positives si 
est pair et négatives si est impair.
