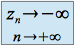Opérations sur les limites
Théorèmes
Fondamental : Théorème
Si ![]() et
et ![]() sont deux suites numériques qui convergent respectivement vers
sont deux suites numériques qui convergent respectivement vers ![]() et
et ![]() alors
alors
La suite
 définie par
définie par 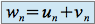 converge vers
converge vers 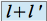
La suite
 définie par
définie par 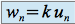 (
(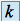 réel fixé) converge vers
réel fixé) converge vers 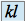
La suite
 définie par
définie par 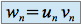 converge vers
converge vers 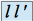
La suite
 définie par
définie par 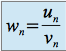 converge vers
converge vers 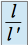 si
si 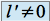
Fondamental : Théorème
Si ![]() et
et ![]() alors
alors
La suite
 définie par
définie par 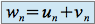 est telle que :
est telle que : 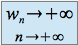
La suite
 définie par
définie par 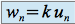 (
(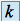 réel fixé) est telle que :
réel fixé) est telle que :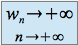 si
si 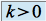 et
et 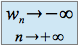 si
si 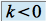
La suite
 définie par
définie par 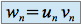 est telle que :
est telle que : 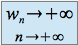
On obtient des résultats analogues lorsque ![]() et
et ![]()
Fondamental : Théorème
Si ![]() et
et ![]() alors
alors
La suite
 définie par
définie par 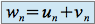 est telle que :
est telle que : 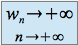
La suite
 définie par
définie par 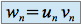 est telle que :
est telle que : 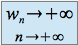 si
si 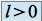 et
et 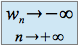 si
si 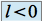
Fondamental : Théorème
Si
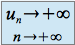 alors la suite
alors la suite  définie par
définie par 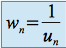 est telle que :
est telle que : 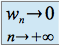
Si
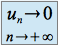 et si
et si  à partir d'un certain rang, alors la suite
à partir d'un certain rang, alors la suite  définie par
définie par 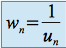 est telle que :
est telle que : 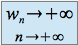
Remarques - formes indéterminées
Remarque :
Si
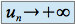 et
et  , on ne peut pas conclure immédiatement pour la suite
, on ne peut pas conclure immédiatement pour la suite  définie par
définie par 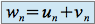
Si
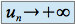 (ou
(ou 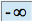 ) et
) et  , on ne peut pas conclure immédiatement pour la suite
, on ne peut pas conclure immédiatement pour la suite
 définie par
définie par 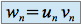
Si
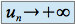 (ou
(ou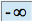 ) et
) et 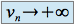 (ou
(ou 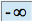 ), on ne peut pas conclure immédiatement pour la suite
), on ne peut pas conclure immédiatement pour la suite  définie par
définie par 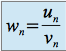
Si
 et
et  , on ne peut pas conclure immédiatement pour la suite
, on ne peut pas conclure immédiatement pour la suite  définie par
définie par 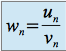
Exemple
Exemple :
Soit ![]() et
et ![]()
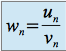 est une forme indéterminée,
est une forme indéterminée,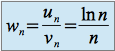 donc
donc 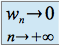
 est une forme indéterminée,
est une forme indéterminée,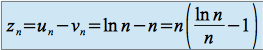
Donc
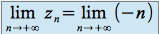 et donc
et donc