Suites croissantes, suites décroissantes
Définition :
Une suite 
est croissante si et seulement si , pour tout entier naturel 
, on a : 
.
Une suite est décroissante si et seulement si, pour tout entier naturel , on a : 
.
On dit que est monotone si elle est croissante, ou si elle est décroissante.
Pour étudier la monotonie des suites on utilise essentiellement les méthodes suivantes :
Technique algébrique
Elle consiste :
soit à étudier le signe de
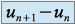
soit à comparer
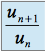à 1, si l'on sait que 
est strictement positif pour tout .
Exemple :
soit définie sur 
par : 
On a : 
Pour tout entier naturel, 
,
et donc 
ou encore : 
.
Donc est croissante.
Technique fonctionnelle
Elle s'applique aux suites de la forme 
. On utilise le sens de variation de la fonction 
.
Exemple :
soit définie sur par :
est définie à partir de la fonction 
. est croissante sur 
.
Donc est croissante.
Technique par récurrence
Elle s'applique aux suites de la forme : 
.
Exemple :
Prouver que la suite définie sur par : 
et 
est strictement croissante.
La propriété est vraie pour
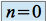, en eff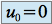et et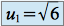 
, donc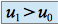 
Supposons la propriété vraie au rang
, c'est à dire : 
On a :
Donc
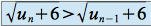, car la fonction 
est croissanteDonc
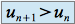
la suite
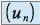est donc strictement croissante.
