Limite d'une suite
Définition
Définition :
Soit 
une suite numérique et 
un réel. On dit que converge vers (ou a pour limite ) si tout intervalle ouvert contenant , contient tous les termes de la suite à partir d'un certain rang.
Autrement dit :
,
On note 
ou encore
Si la suite ne converge pas, on dit qu'elle est divergente.
Remarque :
Remarque :
Si une suite est convergente, sa limite est unique.
Exemple
Exemple :
Soit 
, on a 
En effet 
Et donc 
Plus généralement
Les suites définies, pour 
, par : 
, (
) ont pour limite 0
Suite de limite infinie
Définition :
Soit une suite numérique et 
un réel positif choisi aussi grand qu'on le veut. On dit que admet pour limite 
si tout intervalle de la forme 
contient tous les termes de la suite à partir d'un certain rang.
Autrement dit : 
On note _
ou encore 
De même :
admet pour limite 
On note 
ou encore
Lorsque la suite admet pour limite [respectivement 
], on dit qu'elle diverge vers [respectivement ]. Mais attention, une suite peut être divergente pour deux raisons :
soit sa limite est
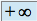ou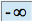
soit elle n'a pas de limite : par exemple la suite
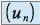définie par : 
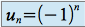est une suite alternée, chaque terme est égal à 1 si 
est pair ou (-1) si est impair ; elle n'a pas de limite, on dit qu'elle diverge.
Remarque : Important
Les suites définies, pour 
, par : 
, () ont pour limite
