Suites majorées, minorées
Définition :
Soit 
une suite numérique.
La suite est majorée si et seulement s'il existe un réel 
tel que 
, pour tout entier naturel 
.
La suite est minorée si et seulement s'il existe un réel
tel que 
, pour tout entier naturel .
Remarque : Note
Si est, à la fois majorée et minorée on dit qu'elle est bornée.
Pour prouver qu'une suite est majorée ou minorée on utilise essentiellement les méthodes suivantes :
Exemple
Exemple :
Prouver que la suite définie sur 
par 
est telle que : 
Le tableau de variation de la fonction 
montre que cette fonction est croissante sur 
, passe par un maximum égal à 
, et décroît vers 0.
De plus 
. On peut donc affirmer que pour entier supérieur ou égal à 1, on a :
Exemple
Exemple :
Prouver que la suite définie sur
par : 
et 
est telle que : 
On résonne par récurrence
La propriété est vraie pour
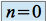, en eff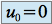et et 
Supposons la propriété vraie au rang
, c'est à dire :
On a : 
Donc 
, car la fonction 
est croissante
Donc 
, et donc 
.
la suite
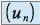est donc telle que .
