Suites adjacentes
Définition :
On dit que les deux suites numériques 
et 
sont adjacentes lorsque la suite est croissante, la suite est décroissante et 
Fondamental : Théorème
Si deux suites numériques et sont adjacentes et telles que la suite est croissante et la suite est décroissante, alors elles convergent vers la même limite 
, et, pour tout 
on a : 
Soit 
On a : 
Or la suite est croissante et la suite est décroissante
donc 
est la somme de deux termes négatifs
et donc 
La suite 
est donc décroissante et converge vers 0, ce qui permet de dire que tous les termes de suite sont positifs.
On en déduit que 
, soit 
Or est décroissante, donc, pour tout , 
et donc
est donc une suite croissante et majorée (par 
).
est donc convergente vers .
On montre de même que est décroissante et minorée (par 
). est donc convergente vers 
.
On en déduit que 
Or 
Donc
Exemple
Exemple :
Soient les suites et définies par :
et
On a :
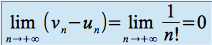
La suite
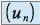est croissante (évident)La suite
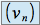est décroissante
En effet : 
soit 
C'est à dire : 
Enfin 
. Et ce nombre est négatif pour 
.
Les suite et sont donc adjacentes, elles convergent vers la même limite , et, pour tout on a :
