AN59
Question
On note
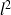l'ensemble des suites
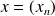de nombres complexes telles que la série
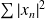converge.
Démontrez que
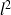est un sous-espace vectoriel de l'espace vectoriel des suites de nombres complexes.Démontrez que pour
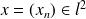et
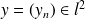, la série
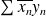converge.On pose
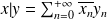.Démontrez que l'on définit ainsi un produit scalaire dans
.
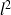On suppose que
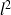est muni de ce produit scalaire et de la norme associée.Soit
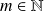. Pour tout
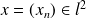, on pose
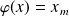. Démontrez que
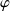est une application linéaire et continue de
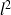dans
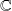et calculez
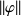, où
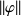désigne la norme usuelle dans l'espace vectoriel des applications linéaires et continues de
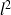dans
.
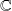