AN58
Question
On note
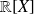l'espace vectoriel des polynômes à coefficients réels. Pour tout polynôme
,
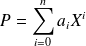désignant le degré de
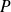, on pose :
Démontrez succinctement que
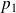et
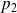sont des normes sur
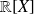.Démontrez que tout ouvert pour la norme
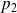est un ouvert pour la norme
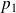.Démontrez que les normes
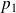et
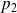ne sont pas équivalentes.
On note
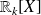le sous-espace vectoriel de
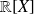constitué par les polynômes de degré inférieur ou égal à
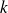. On note
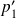la restriction de
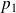à
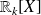et
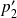la restriction de
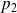à
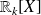.Les normes
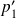et
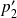sont-elles équivalentes ?
