Chaine finie de masses et ressorts
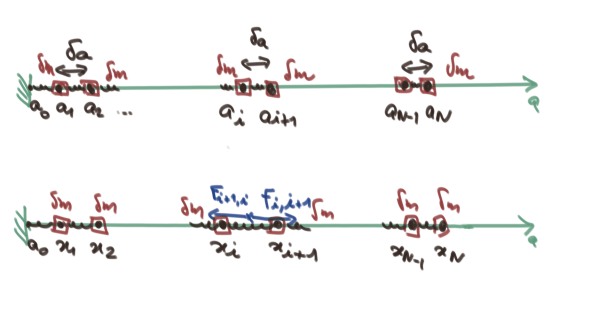
On considère une chaine de ressorts de longueurs \(\delta a\) au repos reliant des masses \(\delta m\) dont les extrémités sont en \(a_i\) pour \(i=1,2..., N\). On suppose que \(N\) tend vers l'infini avec \(L= N\, \delta a\), la longueur de la chaine et \(\rho = \delta m / \delta a\), sa masse linéique, constants. Dans cette limite, les déplacements sont représentés par un champ continu \(\xi(a,t)\) résultant de la discrétisation \(\xi_i(t)= \xi(a_i,t)\).
Rappel : Principe fondamental de la dynamique
Les forces intérieures dans les ressorts vérifient les lois de comportement \(F_{i,i+1}=\alpha \, \xi_{i,i+1}\) avec \( \xi_{i,i+1}=\xi_{1+1} - \xi_i\). Le principe fondamental appliqué aux masses \(i=2,3...,N-1\) s'écrit :
Méthode : Équation du mouvement
En utilisant la relation \(\delta m = \rho \, \delta a\) et la représentation continue du déplacement, l'équation du mouvement pour \(i=2,3...,N-1\) s'écrit :
Nous allons montrer que le passage à la limite \(\delta a \to 0\) conduit à une équation aux dérivées partielles.