AG13
Question
Soit
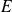un espace vectoriel de dimension
sur
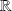. On note
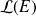l'ensemble des endomorphismes de
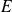et
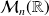l'ensemble des matrices carrés
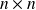à coefficients réels. On admet que
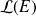muni des lois
et
est un anneau, et que
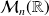muni des lois
et
est un anneau.
Précisez l'élément neutre pour la loi
dans
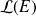et l'élément neutre pour la loi
dans
.
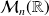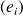désignant une base de
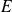, on pose, pour tout
de
,
(
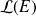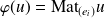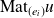désignant la matrice de
dans la base
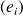).Démontrez que
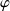est un isomorphisme d'anneau de
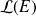dans
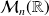.Démontrez que, pour tout
.
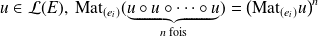