AG12
Question
Soit
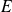un espace vectoriel de dimension
sur
,
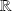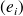une base de
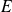et
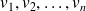
vecteurs de
.
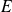Démontrez qu'il existe un unique endomorphisme
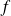de
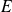tel que,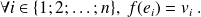 
On note
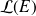l'espace vectoriel des endomorphismes de
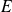, et
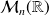l'espace vectoriel des matrices carrées
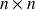à coefficients réels. Pour tout
de
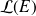, on pose :
(
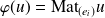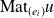désignant la matrice de
dans la base
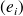).Démontrez que l'application
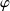de
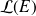dans
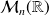est linéaire et bijective.Déterminez la dimension de l'espace vectoriel
.
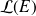