Cas particulier : f est un produit de fonction sin ou cos et d'exponentielle
Propriété
Pour rechercher une solution particulière, on pose 
dans l'équation complète, et on est ramené au cas précédent.
Exemple
Résoudre 
Recherche de la solution de l'équation homogène associée :
L'équation caractéristique obtenue en recherchant une solution du type 
est :
Cette équation du second degré admet deux solutions complexes conjuguées : 
et 
. La solution de l'équation sans second membre est donc :
où 
et 
sont des constantes réelles.
Détermination d'une solution particulière de l'équation
Dans l'équation avec second membre, posons 
On obtient
puis :
En injectant ces relations dans l'équation, on obtient :
soit :
Soit l'équation intermédiaire :
L'équation homogène associée est : 
L'équation caractéristique est : 
Cette équation du second degré admet deux solutions complexes conjuguées : 
et 
n'est pas solution de l'équation sans second membre. On recherche donc une solution particulière du type :
On a
et
L'équation appliquée à 
conduit à l'égalité valable quelque soit 
:
Soit :
Il faut donc
La solution particulière de l'équation intermédiaire est donc :
La solution particulière de l'équation initiale est donc :
Solution générale de l'équation est donc
où et sont des constantes réelles.
Exemple
Résoudre 
Recherche de la solution de l'équation homogène associée
On a montré que la solution de l'équation sans second membre est
où et sont des constantes réelles.
Détermination d'une solution particulière de l'équation
Dans l'équation avec second membre, posons 
On obtient :
puis :
En injectant ces relations dans l'équation, on obtient :
soit :
Soit l'équation intermédiaire 
L'équation homogène associé est : 
L'équation caractéristique est : 
Cette équation du second degré admet deux solutions complexes conjuguées : 
et 
est solution de l'équation sans second membre. On recherche donc une solution particulière du type :
On a
et
L'équation appliquée à conduit à l'égalité valable quelque soit :
Soit :
Il faut donc :
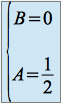
La solution particulière de l'équation intermédiaire est donc :
La solution particulière de l'équation initiale est donc :
Solution générale de l'équation est donc
soit :
où et sont des constantes réelles.
