Cas particulier : f est une fonction exponentielle
Propriété
si
n'est pas solution de l'équation caractéristique, on cherche une solution particulière du type 
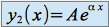
si
est racine d'ordre 
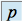de l'équation caractéristique on cherche 
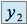tel que 
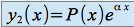où 
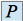est un polynôme de degré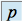
Exemple
Exemple :
Résoudre l'équation différentielle du second ordre
avec les conditions initiales
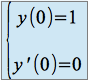
Solution :
Nous devons d'abord chercher la solution de l'équation homogène, soit :
L'équation caractéristique s'écrit :
Elle a pour racine 
et 
. La forme générale des solutions est donc :
où 
et 
sont des constantes réelles.
Il faut maintenant déterminer une solution particulière. 
étant une des fonctions génératrices de 
, la solution particulière recherchée est du type : 
où 
est un polynôme de degré 1, soit :
Dans ce cas :
En injectant ces relations dans l'équation différentielle, nous obtenons :
On a donc :
Soit
d'où :
Dans la mesure où nous recherchons une solution particulière, on prend la fonction pour laquelle 
, soit :
La solution de l'équation est donc :
soit :
Les constantes et sont déterminées à partir des conditions aux limites. Il faut pour cela calculer la dérivée de 
:
Le système à résoudre est
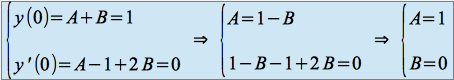
La solution recherchée est donc : 
Exemple
Résoudre 
Recherche de la solution de l'équation homogène associée à :
L'équation caractéristique obtenue en recherchant une solution du type 
est :
Cette équation du second ordre admet une racine double : 
La solution de l'équation sans second membre est donc :
où 
et 
sont des constantes réelles.
Détermination d'une solution particulière de l'équation
Le second membre est une combinaison linéaire d'un polynôme d'ordre 2 et d'une fonction exponentielle. On recherche comme solution particulière du type :
On a
et
L'équation appliquée à conduit à l'égalité variable quelque soit 
:
soit
d'où
La solution particulière recherchée est donc :
La solution générale de l'équation est donc :
où et sont des constantes réelles.
