Cas particulier : f est est un polynôme de degré n
Propriété
Fondamental : Propriété
Si
est un polynôme de degré 
avec 
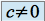et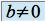 
, on peut montrer qu'une solution particulière 
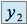est un polynôme de même degré.
Si
est un polynôme de degré avec 
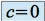et 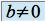alors une solution particulière 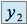est un polynôme de degré 
.
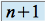Il suffit d'identifier les coefficients du polynôme en calculant 
et 
et en les introduisant dans l'équation différentielle.
Exemple
Exemple :
Résoudre l'équation différentielle du second ordre
Recherche de l'équation homogène associée
L'équation caractéristique obtenue en recherchant une solution du type 
est :
Cette équation du second ordre admet deux solutions réelles : 
et 
. La solution de l'équation sans second membre est donc :
où 
et 
sont des constantes réelles.
Détermination d'une solution particulière de l'équation
Le second membre est un polynôme de degré 1. On cherche comme solution particulière un polynôme de même degré, soit 
et
L'équation appliquée à conduit à l'égalité valable quelque soit 
:
d'où :
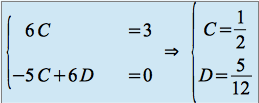
Une solution particulière est donc :
La solution générale de l'équation peut donc s'écrire : 
où et sont des constantes réelles.
