Equations linéaires homogènes à coefficients constants
Introduction
On cherche ici à déterminer la solution des équations différentielles du type :
où 
, 
et 
sont des constantes et 
.
On cherche une solution du type :
Le développement de l'équation différentielle avec cette fonction 
, conduit à l'équation caractéristique :
Propriété
Fondamental : Propriété
On distingue trois cas suivant le signe du discriminant (
)
si
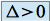, on a deux racines réelles : 
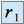et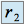 
. La solution générale de l'équation homogène est définie par :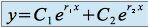
si
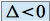, on a deux racines complexes conjuguées : 
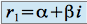et 
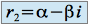. La solution générale de l'équation homogène est définie par :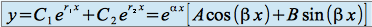
si
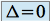, on a une racine réelle double : 
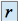. La solution générale de l'équation homogène est définie par :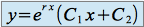
Dans tous les cas, les constantes 
et 
seront fixées par les conditions initiales.
Exercice classique
Exemple :
Résoudre l'équation différentielle du second ordre
avec les conditions :
l'équation caractéristique associée à cette équation est :
Le discriminant (
) est négatif et cette équation admet deux racines complexes : 
et 
. La solution de l'équation est donc :
qui peut s'écrire sous la forme :
On détermine les constantes réelles 
et 
grâce aux conditions aux limites. Pour cela il faut calculer la dérivée de , soit :
Soit :
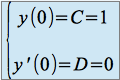
La solution recherchée est donc : 
Exercice classique
Exemple :
Résoudre l'équation différentielle du second ordre
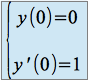
l'équation caractéristique associée à cette équation est :
Le discriminant (
) est positif et cette équation admet deux racines réelles : 
et 
. La solution de l'équation est donc :
On détermine les constantes réelles 
et 
grâce aux conditions aux limites. Pour cela il faut calculer la dérivée de , soit :
Soit :
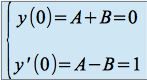
D'où
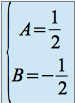
La solution recherchée est donc :
Exercice classique
Exemple :
Résoudre l'équation différentielle du second ordre
avec les conditions :
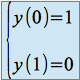
l'équation caractéristique associée à cette équation est :
Le discriminant () est nul et cette équation admet une racine double : 
. La solution de l'équation est donc :
On détermine les constantes réelles et grâce aux conditions aux limites. Soit :
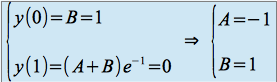
