Définition générale
Définition
Définition :
On appelle équation différentielle linéaire d'ordre 
,(
) , une équation de la forme :
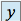est la fonction cherchée
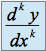est la dérivée 
de 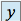par rapport à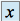 
les fonctions
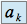sont des fonctions de 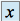et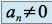 
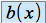est appelé second membre de l'équation
Si les fonctions sont les constantes, alors on dit que l'équation différentielle est à coefficients constants.
Remarque
Remarque :
On rappelle que
Dans la suite, on notera
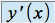la dérivée première de 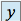par rapport à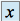
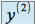ou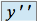 
la dérivée seconde de 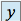par rapport à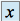
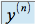la dérivée 
de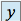 par rapport à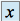
L'équation différentielle sera dite homogène si et seulement si
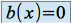
L'équation différentielle sera dite normalisée si et seulement si 
.
Propriété
Fondamental :
L'ensemble des solutions d'une équation différentielle linéaire homogène
est un sous-espace vectoriel de l'ensemble des applications de 
dans . La résolution de l'équation homogène d'ordre suppose donc la détermination de solutions indépendantes 
formant une base du sous-espace vectoriel des solutions. Ainsi, il faudra déterminer autant de solutions que l'ordre de l'équation, la solution générale étant une combinaison linéaire de ces solutions, soit :
La solution des équations peut être explicite, dans ce cas on obtient une relation de type 
ou 
mais elle peut être implicite et conduire à une relation du type 
.
