Développement limité d'une fonction (n + 1) fois différentiable
Soit ![]() un intervalle ouvert de
un intervalle ouvert de ![]() contenant le point
contenant le point ![]() et
et ![]() une fonction
une fonction ![]() fois différentiable sur
fois différentiable sur ![]() .
.
On suppose également qu'il existe un nombre réel ![]() et une constante
et une constante ![]() tel que les relations
tel que les relations ![]() et
et ![]() impliquent
impliquent ![]() .
.
Alors la formule de Taylor fournit le développement limité d'ordre ![]() de la fonction
de la fonction ![]() autour de
autour de ![]() .
.
Démonstration
La formule de Taylor est applicable à ![]() .
.

Pour tout ![]() , vérifiant
, vérifiant ![]()
En posant ![]() , on obtient
, on obtient ![]() .
.
Ainsi ![]()
est le développement limité d'ordre ![]() de la fonction
de la fonction ![]() autour de
autour de ![]() .
.
Remarques
Si
 est continue en 0, pour tout
est continue en 0, pour tout 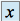 de
de  ,
,  admet un
admet un 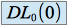 dont la partie principale est
dont la partie principale est 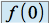 .
.
Si
 est dérivable en 0, pour tout
est dérivable en 0, pour tout 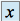 de
de  ,
,  admet un
admet un 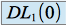 dont la partie principale est
dont la partie principale est 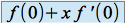 .
.
Une fonction peut admettre un
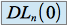 sans être
sans être  fois dérivable en
fois dérivable en  . Ainsi la fonction
. Ainsi la fonction  définie sur
définie sur  par :
par :
admet un
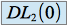 de partie régulière
de partie régulière 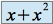 car
car 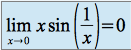 .
.Mais cette fonction n'est pas deux fois dérivable en
 !
!En effet , sa fonction dérivée est donnée par :
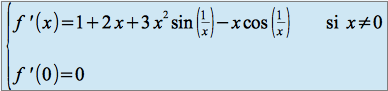
Or
Et
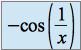 n'admet pas de limite en
n'admet pas de limite en  . Donc
. Donc  n'est pas deux fois dérivable en
n'est pas deux fois dérivable en  .
.





