Opérations algébriques sur les développements limités
Soient 
deux fonctions admettant respectivement comme développement limité d'ordre 
autour de 
:
et
Alors,
pour tout couple de nombres réels
et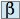 
, la fonction 
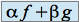admet un 
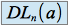dont la partie principale est
la fonction
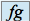admet un 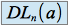dont la partie principale s'obtient en effectuant le produit
et en ne conservant que les termes de degré inférieur ou égal à
.si
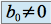, la fonction 
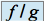admet un 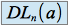dont la partie principale s'obtient en effectuant la division suivant les puissances crois-santes jusqu'à l'ordre de 
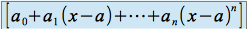par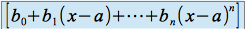 
.
Exemple
Exemple :
Calculer la partie principale du développement limité d'ordre 
autour de 
de la fonction
Nous pouvons utiliser la méthode dite des "coefficients indéterminés".
Désignons par 
le 
. On peut écrire, pour tout 
non nul :
donc par unicité du développement limité
ce qui implique que
soit en résolvant ce système
Nous aurions pu également effectuer la division suivant les puissances croissantes jusqu'à l'ordre de 
par 
.
