4.2 Ondes de détente et méthode des caractéristiques
Pour fixer les idées, on suppose que \(C(\rho)\) est une fonction monotone décroissante de \(\rho\) comme dans l'exemple particulier considéré.
Fondamental :
On considère une condition initiale \(\rho(x,0)=\rho_0(x)\) telle que \(\rho_0(x) = \rho_g$ pour $x\le x_g\) (Gauche) et \(\rho_0(x) = \rho_d$ pour $x\ge x_d\) (Droite). Dans l'intervalle \([x_g,x_d]$, on suppose que $\rho_0(x)\) relie continuement de façon monotone les valeurs \(\rho_g\) et \(\rho_d.\)
On suppose \(\rho_g > \rho_d\) : la circulation devient donc de plus en plus fluide. Les deux hypothèses entraînent que la fonction \(C_0(x) = C[\rho_0(x)]\) est strictement décroissante.
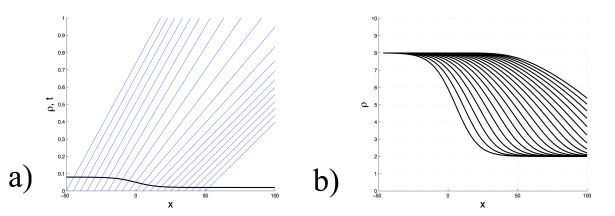
Onde de détente \({\rho_g\over \rho_{\rm max}} =0.75\) et\( {\rho_d\over \rho_{\rm max}} =0.4.\) a) Condition initiale est droites caractéristiques. b) Solution \(\rho(x,t)\) à des instants successifs.
Méthode :
Une représentation graphique du calcul de la solution \(\rho(x,t)\) issue de la condition initiale \(\rho_0(x)\) est obtenue en traçant toutes les caractéristiques dans le plan \((x,t).\) A gauche du plan se trouvent les caractéristiques d'équations\( x = a + C(\rho_g) t\) avec \(a \le x_g\) tandis que l'on trouve à droite les caractéristiques d'équation \(x = a + C(\rho_d) t\) avec \(a \ge x_d.\) Entre ces deux familles se trouvent les droites d'équation \(x = a + C[\rho_0(a)] t$ avec $a \in [x_g, x_d].\) Aucune de ces droites ne se coupent du fait que \(C_0(x)\) est croissante. On dit que l'on est en présence d'une onde de détente.
Remarque :
Dans la limite où \(x_g=x_d=0,\) la condition initiale \(\rho_0(x)\) est discontinue. La solution \(\rho(x,t)\) est cependant continue, et s'obtient en traçant un faisceau de droites caractéristiques centrées en \((x, t) = (0, 0).\) On dit que l'on est en présence d'une onde de détente centrée.