4.1 Du bilan global au bilan local
Définition :
On considère que la fonction \(\rho(x,t)\) est la densité d'automobile sur une route (nombre par unité de longueur) et on note \(Q(\rho)\) le flux d'automobile supposé fonction (continue) de \(\rho\) uniquement. Pour fixer les idées, supposons que \(V(\rho) =V_{\rm max} \left (1 - \rho^2/\rho^2_{\rm max}\right)\) modélise la vitesse des véhicules qui décroît avec la densité \(\rho\) du trafic. Le flux est alors \(Q(\rho) = \rho \; V(\rho) =V_{\rm max} \left( \rho - \rho^3/\rho^2_{\rm max}\right).\) Il est maximal pour \(\rho_* = \rho_{\rm max}/\sqrt 3 \sim 0.6\; \rho_{\rm max}.\)
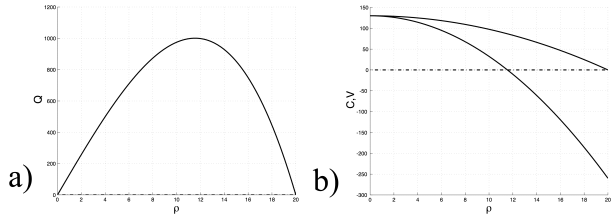
(a) Flux de véhicules \(Q(\rho).\) (b) Vitesses des véhicules \(V(\rho)\) et vitesse d'advection \(C(\rho)=Q'(\rho)\) des fluctuations de la densité de véhicules \(\rho.\)
Le bilan global exprimant la conservation du nombre de véhicules s'écrit
\[\frac{d \, }{dt} \int_{x_1}^{x_2} \rho \; dx + \left[ Q(\rho) \right]_{x_1}^{x_2} = 0 \;,\] |
pour tout intervalle fixe \([x_1,x_2],\) avec la notation \([f]_{x_1}^{x_2} = f(x_2) - f(x_1).\)
On en déduit facilement que les solutions \(\rho(x,t)\) continues dérivables vérifient l'équation de "bilan local''
\[\partial_t \, \rho + \partial_x\,{} Q(\rho) = 0 \;, \] |
où \(\partial_t\) et \(\partial_x\) désignent respectivement les dérivées partielles par rapport au temps et à l'espace.
Fondamental :
On définit la vitesse \(C(\rho) = {Q'( \rho) }= V_{\rm max} \left( 1 - 3 \, \rho^2/\rho^2_{\rm max}\right)\) et l'on
écrit l'équation de bilan local sous la forme
\[\partial_t\, \rho + C(\rho) \; \partial_x\, \rho = 0\;.\] |
On voit alors que le long d'une courbe \(x(t)\) définie par l'équation \(\frac{d \, x}{dt}(t) = C\left\{ \rho[x(t),t]\right\},\) plus simplement notée \(\dot x = C(\rho)$, la grandeur $\rho[x(t),t]\) reste constante (vérification en reportant dans l'équation).
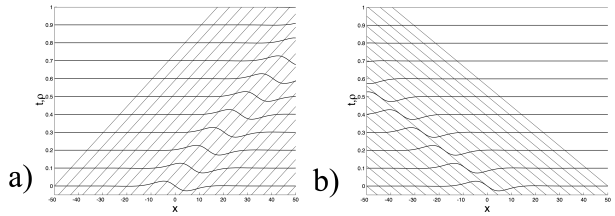
Propagation d'un coup de frein (a) \(\rho_0= 0.4 \;\rho_{\rm max} < \rho_*\) (b) \(\rho_0= 0.75 \;\rho_{\rm max} > \rho_*.\)
Définition :
On dit que les courbes définies par \(\dot x = C(\rho)\) dans l'espace \((x,t)\) sont les "caractéristiques'' de l'équation de bilan et que "l'invariant de Riemann'' le long d'une telle caractéristique est la grandeur \(\rho.\) Pour cet exemple particulier d'équation, les caractéristiques sont toujours des droites. En effet, comme \(\rho\) est constant le long d'une caractéristique, \(C(\rho)\) l'est aussi.
Remarque :
La linéarisation \(\rho= \rho_0 + \widetilde{\rho}\) de l'équation de bilan local autour de l'état de base \(\rho = \rho_0\) conduit (\(\widetilde{\rho}$ petit devant $\rho_0\)) à l'équation
\[\partial_t\, \widetilde{\rho} + C(\rho_0) \; \partial_x\, \widetilde{\rho} = 0 \;.\] |
La relation de (non-)dispersion \(\omega = C(\rho_0)\; k\) met en évidence des ondes (en notation complexe)
\(\widetilde{\rho} = \rho_m \exp (ikx-i\omega t)\) qui se propagent à la vitesse \(C(\rho_0).\)
On peut donc voir les caractéristiques comme des rayons dont la vitesse prend en compte les variations de \(\rho\) dans le cas où les termes non-linéaires ne peuvent plus être négligés.