3.2 Cas particulier c=c(x)
Fondamental :
Dans le cas où \(c(\rho,x,t)=c(x)\) ne dépend ni du temps ni de la variable \(\rho,\) l'équation d'advection s'écrit
\[\frac{\partial \, \rho}{\partial t} + c(x) \; \frac{\partial \rho}{\partial x} = f(\rho,x,t) \;,\] |
avec la condition initiale \(\rho(x,0) = \rho_0(x)\) et le système dynamique s'écrit
\[\left\{ \begin{matrix} \dot x & = & c(x) \cr \dot \rho & = & f(\rho, x, t) \end{matrix} \right. \;, \] |
avec les conditions initiales \([x(0), \rho(0)]=[a, \rho_0(a)].\)
S'il existe des points \(a_i\) pour lesquels \(c(a_i)=0,\) il existe alors des droites caractéristiques \({\cal C}_{a_i}\) d'équations \(x=a_i.\) Dans un intervalle ouvert délimités par ces points, la fonction \(c(x)\) ne s'annule pas et on peut donc considérer la primitive de \(1/c(x)\) définie par
\[\Theta(x) = \int_{x_*}^x {1\over c(s) } \, ds \;, \] |
où \(x_*\) est un point choisi au hasard dans cet intervalle. Cette primitive permet d'exprimer l'équation des courbes caractéristiques sous la forme
\[\Theta[x(t)]- \Theta(a) = t \qquad \Longleftrightarrow \qquad x(t) = \Theta^{-1} \left[\Theta(a) + t\right]\;,\] |
où \(\Theta^{-1}\) est l'inverse de la fonction \(\Theta.\) Cet inverse existe sur l'intervalle considéré dans la mesure où sa dérivée \(1\over c(x)\) ne s'annule pas. On peut alors écrire
\[ X(a,t) = \Theta^{-1} \left[\Theta(a) + t\right] \qquad \Longleftrightarrow \qquad A(x,t) = \Theta^{-1} \left[\Theta(x) - t\right] \;. \] |
On remarque que les courbes caractéristique \({\cal C}_a\) se déduisent les unes des autres par des translations en temps dans le plan \((x,t).\) En effet, on peut écrire \(\Theta\left[x_2(t)\right]- \Theta\left[x_1(t)\right] =\Theta(a_2) - \Theta(a_1).\)
Exemple :
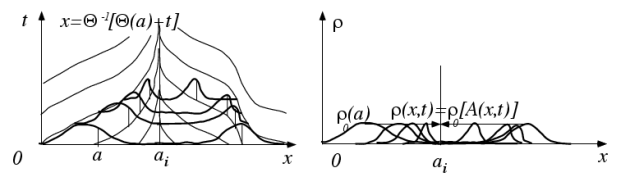
Dans le cas très particulier \(f=0,\) la quantité \(\rho\) est invariante le long des courbes caractéristiques (invariant de Riemann) et la solution sécrit \(\rho(x,t) = \rho_0[A(x,t)]= \rho_0\left\{ \Theta^{-1} \left[\Theta(x) - t\right]\right\}.\)
Courbes caractéristiques dans le cas \(c(x)\) indépendant de \(t\) et de \(\rho\) et solution \(\rho(x,t) =\rho[A(x,t)]\) dans le cas particulier \(f=0.\)
Exemple :
Dans le cas général \(f\ne 0,\) on a \(\rho(x,t) = \rho^{(L)}[A(x,t),t]$ où $\rho^{(L)}(a,t) = \rho_{{\cal C}_a}(t)\) est obtenu en résolvant l'équation :
\[\dot \rho = f\left[ \rho(t), X(a,t), t \right] \;,\] |
avec \(X(a,t) = \Theta^{-1} \left[\Theta(a) + t\right].\) La résolution de cette équation, comme le calcul et l'inversion de la fonction \(\Theta(x),\) nécessitent, la plupart du temps, le recours à des méthodes numériques.