3.1 Cas particulier c=c0
Fondamental :
Dans le cas où \(c(\rho,x,t)=c_0\) est une constante, l'équation d'advection s'écrit
\[\frac{\partial \, \rho}{\partial t} + c_0 \; \frac{\partial \rho}{\partial x} = f(\rho,x,t) \;, \] |
avec la condition initiale \(\rho(x,0) = \rho_0(x)\) et le système dynamique s'écrit
\[\left\{ \begin{matrix} \dot x & = & c_0 \cr \dot \rho & = & f(\rho, x, t) \end{matrix} \right. \;, \] |
avec les conditions initiales \([x(0), \rho(0)]=[a, \rho_0(a)]\). On en déduit alors
\[x = X(a,t) = a + c_0 \; t \qquad {\rm et } \qquad \dot \rho = f[\rho(t), a+c_0\; t, t] \;. \] |
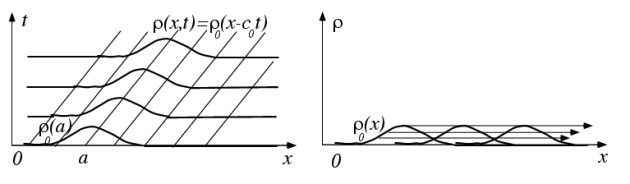
Les caractéristiques \({\cal C}_a\) sont donc des droites parallèles de pente \(1/c_0\) dans le plan \((x,t).\)
Exemple :
Dans le cas très particulier f=0, la quantité \rho est invariante le long de ces droites caractéristiques et l'on peut écrire \(\rho^{(L)}(a,t) = \rho_{{\cal C}_a}(t) = \rho_0(a)\). On en déduit \(\rho(x,t) = \rho_0(x-c_0\,t)\) en utilisant la relation \(a=A(x,t) = x-c_0\, t\) qui inverse la relation \(x=X(a,t) =a + c_0\,t.\) On vérifie alors que l'on a bien \(\frac{\partial\, \rho}{\partial t}+ c_0 \;\frac{\partial \rho}{\partial x}= 0.\) Dans le cadre de la méthode des caractéristiques, la quantité invariante \(\rho\) est apellée "invariant de Riemann''.
Exemple :
Dans le cas général \(f\ne 0,\) la solution est \(\rho(x,t) = \rho^{(L)}(x-c_0\,t,t)$ où $\rho^{(L)}(a,t) = \rho_{{\cal C}_a}(t)\) est obtenue en résolvant l'équation différentielle ordinaire
\[\dot \rho = f[\rho(t), a+c_0\,t ,t]\; . \] |
Sauf dans des cas où l'on peut trouver une résolution analytique, il faut recourir à une méthode numérique (par exemple avec un schéma de Runge-Kutta) pour résoudre cette équation. Dans le cadre de la méthode des caractéristiques la quantité \(\rho_{{\cal C}_a}(t)\) ainsi trouvée est appellée "fonction de de Riemann''.