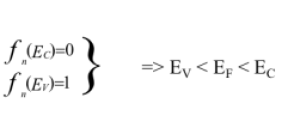II.1 Répartition des porteurs sur les états quantiques, Niveau de FERMI

Fondamental

Les répartitions des porteurs dans les bandes d'énergie répondent à des lois statistiques.

Ainsi, la répartition des électrons sur les niveaux d'énergie suit la statistique de FERMI-DIRAC :

La probabilité de présence d'un électron sur un niveau énergétique E sera notée f n ( E ) f_{n} ( E )

Elle est donnée par la formule : f n ( E ) = 1 1 + exp ( E − E F kT ) f_{n} ( E ) = {1} over { 1+exp ( {E- E_{F}} over {kT} ) }

k = constante de Boltzmann.

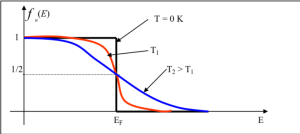
Cette expression fait apparaître un niveau énergétique EF qui correspond à une probabilité de présence égale à ½ :

f n ( E f ) = 1 2 f_{n} ( E_{f}) = 1 over 2

Ce niveau correspond, au zéro absolu, à la séparation entre les niveaux vides et les niveaux pleins. On parle parfois « d'énergie moyenne » ou de « taux moyen de remplissage » ou plus souvent de niveau de FERMI.

Si on trace la fonction correspondante, on obtient :

Pour une température égale à 0K (en noir sur la figure)

Pour une température T1(en rouge sur la figure)

Pour T2 > T1 (en bleu sur la figure)

On pourra remarquer que, quelle que soit la température :

Illustration niveau de FERMI

f n ( E f ) = 1 2 f_{n} ( E_{f}) = 1 over 2

Dans le cas de matériaux semi-conducteurs, on peut assurer que le niveau de FERMI se trouve dans la bande interdite. En effet, au zéro degré absolu, la bande de valence est pleine et la bande de conduction vide.

En considérant que le niveau de FERMI est situé au milieu de la bande interdite, ce que nous justifierons plus loin, on peut calculer la probabilité de présence d'un électron sur le niveau EC pour différentes températures.

ExempleExemple du Silicium :

Eg = 1,12 eV

k = 8,619 10–5 eV/K

Ces probabilités de présence sont donc très faibles et varient énormément en fonction de la température.

Remarque

Le calcul précédent amène à une conclusion très intéressante; on peut remarquer que, quelle que soit la température, le terme exp ( E − E F kT ) exp ( {E- E_{F}} over {kT} ) est toujours très grand devant 1.

On peut donc simplifier la fonction probabilité de présence qui devient :

f n ( E ) = 1 1 + exp ( E − E F kT ) E ≫ E F → exp − ( E − E F kT ) f_{n} ( E ) = {1} over { 1+exp ( {E- E_{F}} over {kT} ) } binom{E>> E_{F}}toward exp {-({E- E_{F}}over {kT})}

pour E>>EF

Fondamental

La statistique de FERMI-DIRAC se ramène donc, pour E>EF, à la statistique dite de BOLTZMANN (statistique des gaz parfaits). Ce sera vrai pour tous les Semi-conducteurs que l'on pourra assimiler à des gaz parfaits de ce point de vue.

On a de même, pour E<<EF

f n ( E ) = 1 1 + exp ( E − E F kT ) E ≪ E F → 1 − exp ( E − E F kT ) f_{n} ( E ) = {1} over { 1+exp ( {E- E_{F}} over {kT} ) } binom{E<<E_{F}}toward1-exp({E- E_{F}}over {kT})