Jonction de deux ressorts

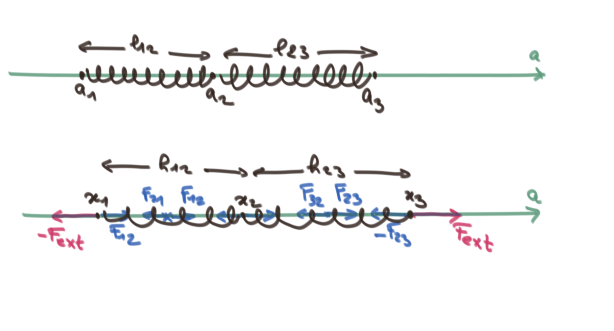
On considère deux ressorts de coefficient \(\alpha\) identiques, mis bout à bout, dont les longueurs respectives sont \(l_{12}\) et \(l_{23}\) et dont les extrémités sont situées aux abscisses \(a_1\), \(a_2\) et \(a_3\). On applique respectivement les forces \(-F_{ext}\) et \(F_{ext}\) aux extrémités \(a_1\) et \(a_3\). On note \(x_1\), \(x_2\) et \(x_3\) les nouvelles positions des extrémités après la déformation qui résulte de la contrainte extérieure imposée.

DéfinitionAllongements et forces intérieures

On note \(\xi_1 = x_1-a_1\), \(\xi_2 = x_2-a_2\) et \(\xi_3 = x_3-a_3\) les déplacements des extrémités et \(\xi_{12} = \xi_2-\xi_1\) et \(\xi_{23} = \xi_3-\xi_2\) les allongements des ressorts.

En notant \(F_{12}\) et \(F_{23}\) les intensités des forces intérieures respectives dans les ressorts, on a \(F_{ext} = F_{12} = F_{23} =- F_{21} =- F_{32}\).

MéthodeLoi de comportement du système global

La loi de comportement élastique appliquée à chacun des ressorts s'écrit :

\[F_{12} = \alpha \; \Delta_{12} \qquad \hbox{et} \qquad F_{23} = \alpha \; \Delta_{23} \]
\[\qquad \hbox{avec} \qquad \Delta_{12} = {h_{12} - l_{12} \over l_{12} } = {\xi_{12} \over l_{12}} \qquad \hbox{et} \qquad \Delta_{23} = {h_{23} - l_{23} \over l_{23} } = {\xi_{23} \over l_{23}} \;. \]

On en déduit \(l_{12} \, F_{12} + l_{23} \, F_{23}  = \alpha \, (\xi_{12} + \xi_{23})= \alpha \, \xi_{13}\) où \(\xi_{23} = \xi_{12} + \xi_{23} = \xi_3 - \xi_3\) est l'allongement du système global constitué de la jonction des deux ressorts. La loi de comportement du système global obéit à la même loi que celle d'un ressort unique :

\[F_{ext} = F_{13} = \alpha \; \Delta_{13} \qquad \hbox{avec} \qquad \Delta_{13} = {\xi_{13} \over l_{13}}\;.\]

Ce résultat peut paraitre trivial dans la mesure où la jonction de deux ressorts de coefficient \(\alpha\) commun peut être considéré comme un ressort unique. On remarque toutefois que la forme usuelle \(F_{ext}= k \,\xi_{13}\), où \(k\) est la constante de raideur, doit prendre en compte la relation \(k= \alpha / l\) : la constante de raideur d'un ressort est inversement proportionnelle à sa longueur.