Résolutions dans C des éq. du second degré à coef. réels.
Rappel :
On rappelle qu'une équation de degré n a n racines dans
.
Méthode :
On se propose de résoudre dans
toute équation de type
où a,b et c sont des
nombres réels
. La factorisation canonique effectuée dans
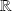reste valable dans
.
Si
, alors on sait résoudre l'équation dans
.
Si
:
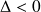Elle admet deux solutions complexes conjugués :
Dans le cas
, alors on rappelle que l'équation admet deux racines réelles :
Dans tous les cas, on aura les deux propriétés suivantes :
• La somme des racines
• Le produit des racines
