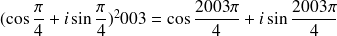Forme trigonométrique d'un produit et formule de Moivre
Méthode :
Soit
, alors on remarque que :
Soit
D'où
Donc
.
L'application de cette propriété conduit à la formule de Moivre :
Exemple :
On aura donc par exemple :
