Forme trigonométrique
Définition :
Le module de
, noté
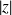, est défini comme la norme du vecteur
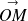. Or les coordonnées de ce vecteur sont
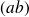, donc :
Définition :
L' argument de z est la mesure (en radians) de l'angle entre l'axe des
et
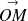. Cet angle est définit à
près . Pour
, l'argument n'est pas défini. Sinon, on utilisera, toujours avec les notations de la figure 1-5.3 :
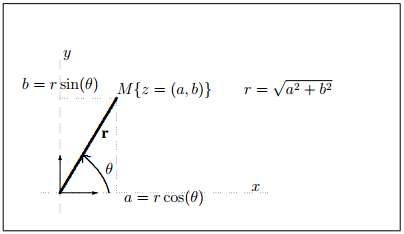
FIGURE 1-5.3 – Représentation trigonométrique d'un nombre complexe z(a,b)
Remarque :
Tout nombre complexe non nul
de module
et d'argument θ peut donc s'écrire sous la forme
