Racine de l'unité dans C
Rappel :
La notation complexe est utile pour résoudre
.
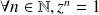En effet, on remarque que
et que
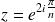est une racine
de l'unité.
Les autres racines sont obtenues par multiplication par z.
Les n racines
de l'unité sont donc :
Elles se placent dans le plan complexe sur le cercle de rayon 1 centré sur l'origine et sont espacées d'un angle
La racine troisième de l'unité est noté j (cf. figure 1-11.5).
On a
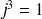et comme propriété remarquable :
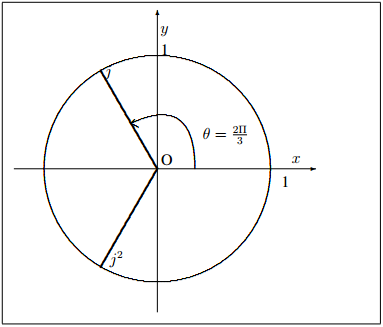
FIGURE 1-11.5 – Racine troisième de l'unité.
La notation complexe est utile pour résoudre :
Les n racines
de re^{i\theta} sont :
Remarque :
On remarque que l'on obtient toutes les racines
de
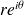en multipliant successivement
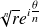par les racines
de 1
