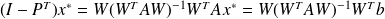Techniques for multiple right-hand sides
Preconditioning techniques considered (I)
We consider techniques to precondition or improve an existing preconditioner second level preconditioning
Solve
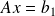and extract information 
Use
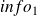
and extract information 
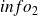
Use
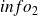
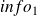
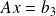and ......
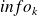
residuals;
descent directions;
steps;
or other vectors such as eigenvectors of
...
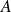Preconditioning techniques considered (II)
We study and compare two approaches :
Deflation [Frank, Vuik, 2001].
Limited Memory Preconditioners (LMP): Preconditioners based on a set of A-conjugate directions.
Generalization of known preconditioners: spectral [Fisher, 1998], L-BFGS [Nocedal, Morales, 2000], warm start [Gilbert, Lemar´echal, 1989].
we cover:
Theoretical properties.
Numerical experiments (data assimilation).
Properties
Deflation Techniques
Given
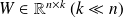formed with \cre{appropriate information} obtained when solving the previous system.Consider the
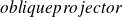
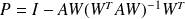.Split the solution vector as follows
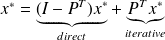.Compute
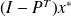with
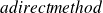.Compute
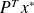with an iterative method.
Some Properties (Deflation)
Computation of
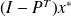: Computation of
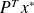:Any solution} of the compatible singular system
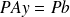satisfies
.
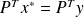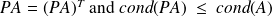. Use CG with
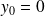to solve
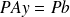and compute
.
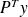Limited Memory Preconditioners (LMP)
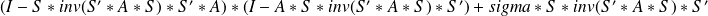
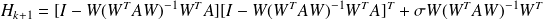
with
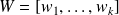.Particular forms
The
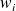's are the descent directions obtained from CG:
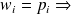L-BFGS preconditioner.The
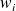's are eigenvectors of
:
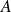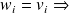spectral preconditioner.The
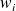's are Ritz-vectors of
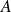wrt an orthognal basis
:
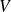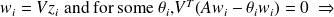Ritz preconditioner.
Spectral Properties for LMP (I)
Fundamental : Theorem
The spectrum
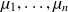of the preconditioned matrix
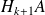satisfies} :
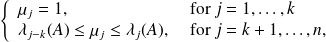
Note: the matrix A to precondition is the same (only the RHS changes).
Proof
Assume that the
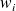have been normalized, without loss of generality :
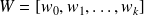
with
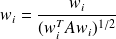. Let
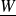, be the
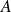-conjugate complement of
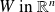. The following conjugacy relations hold :
.
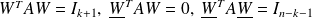We have
.
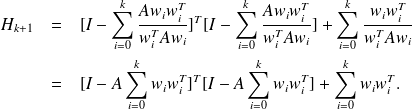This can be rewritten in terms of matrices
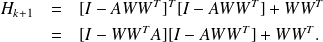
It can be shown as follows that
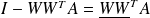. Using the conjugacy relations, we have
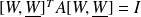and since
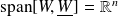, the matrix
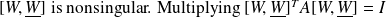left by
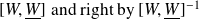yields
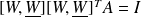which is equivalent to
.
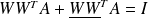Therefore
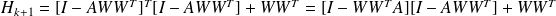writes
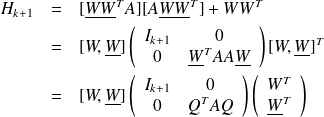
The matrix
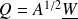is an orthogonal matrix of
. Since
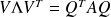with
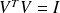, is a spectral decomposition of the matrix
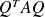, we have
.
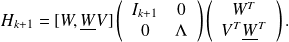The matrix
has the same spectrum as the matrix
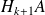and can be written
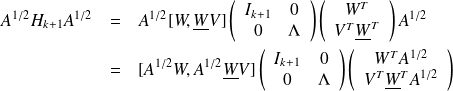
This is a diagonalization of the matrix
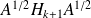, because
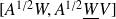is orthogonal. The result follows from (see Horn anf Johnson)
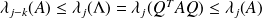with
.
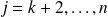Spectral properties for LMP (II)
nn
Existence of a factored form for the LMP (not the Cholesky factor !)
L-BFGS :
A
is
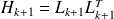where :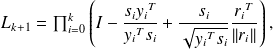
with
and
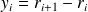.Same cost in memory and CPU as the unfactored form.
Spectral :
A possible factored form is
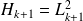where :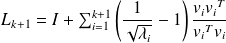
Same cost in memory as the unfactored form.
Why looking for a factored form H = LLT ?
With a non factored form, we use CG preconditioned by H.
With a factored form, we solve
.
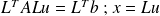:When accumulating preconditioners, symmetry and positiveness are still maintained :
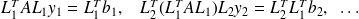
Least-squares
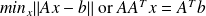:LSQR (or CGLS) is more accurate than CG in presence of rounding errors but works with
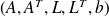instead of
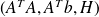.More appropriate if reorthogonalization of the residuals is used.
Experiments with LSQR
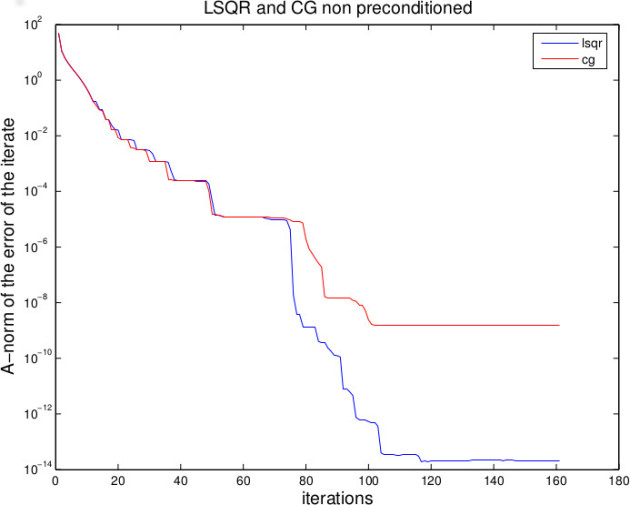
LSQR is better than CG !
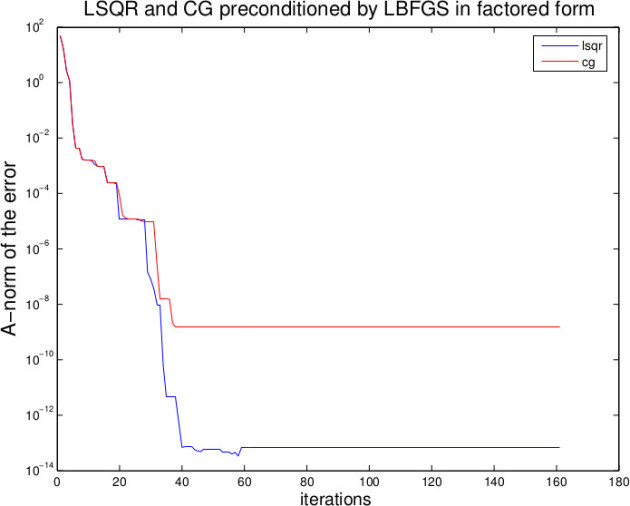
LSQR is again better than CG !
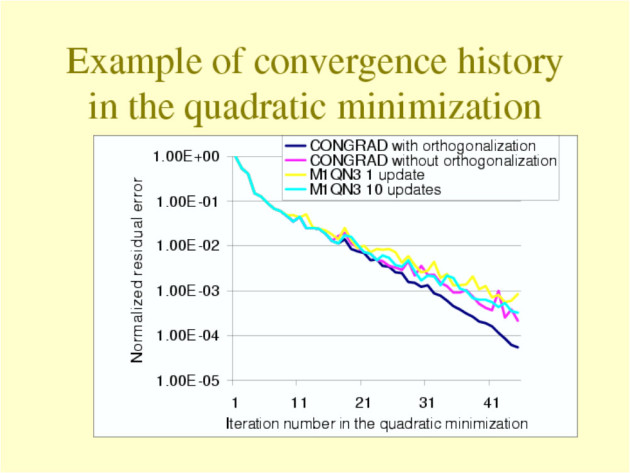
Why to reorthogonalize the residuals ?
In finite precision, residuals often loose}orthogonality (or conjugacy) and theoretical convergence is then slowed down.
Reorthogonalization of residuals in CG is terribly successful} when matrix-vector product is very expensive compared to other computations in CG (see example in the next slide).
Note: to restore orthogonality or conjugacy, working with
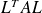and the canonical inner-product is better (memory, CPU, error propagation) than working on
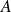preconditioned by
.
Example of reorthogonalization effect : CERFACS data assimilation system (1 000 000 unknowns)
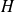Experiments
Experiments with a data assimilation problem
Problem formulation : nonlinear least-squares problem
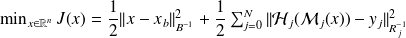
Size of real (operational) problems :
,
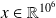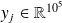
The observations
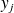are noisy.Solution strategy : Incremental 4DVAR (i.e. inexact/truncated Gauss-Newton algorithm).
Main ingredients
Sequence of linear symmetric positive definite systems to solve :
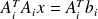
Whose matrix varies.
Experiments description
Algorithmic variants tested :
Use CG to solve the normal equations.
Compare with Deflation (spectral) 3 LMP preconditioning techniques :
Ritz technique (
"using Ritz information"
).Spectral preconditioner (
"using spectral info."
).L-BFGS preconditioner (
"using descent directions"
).
Where spectral information is needed, use Ritz (vectors) as approximations of the eigenvectors.
Ritz vectors are obtained by mean of a variant of CG : the Lanczos algorithm which combines linear and eigen solvers.
Experiment large system OPA VAR
OPA ocean general circulation model.
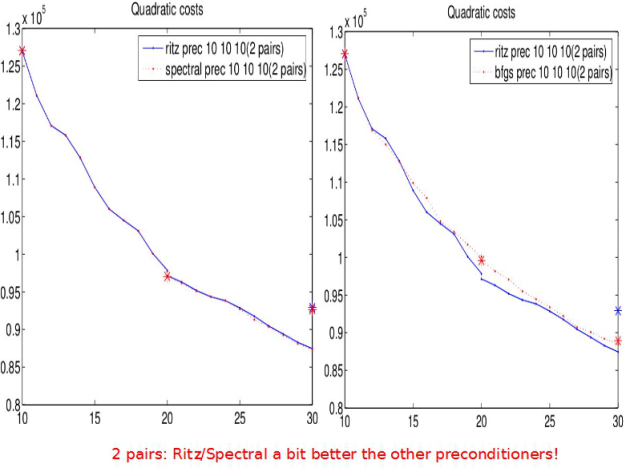
Comparison of the effect on the second quadratic minimization (the first is used to obtain the information).
Comparison of the quadratic/Nonlinear cost. Information : the 10 vectors obtained using the first outer-loop (10 cg steps).
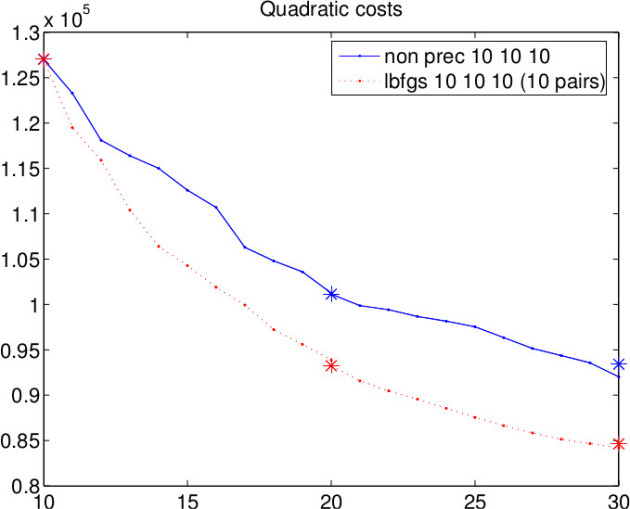
L-BFGS better than no preconditioning
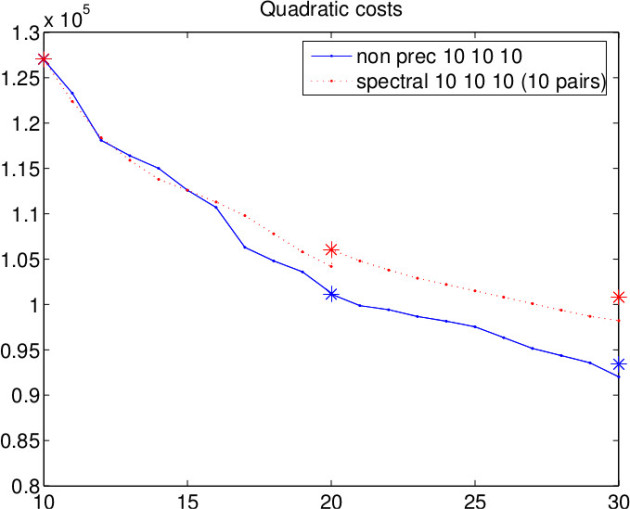
Spectral is worse than no preconditioning
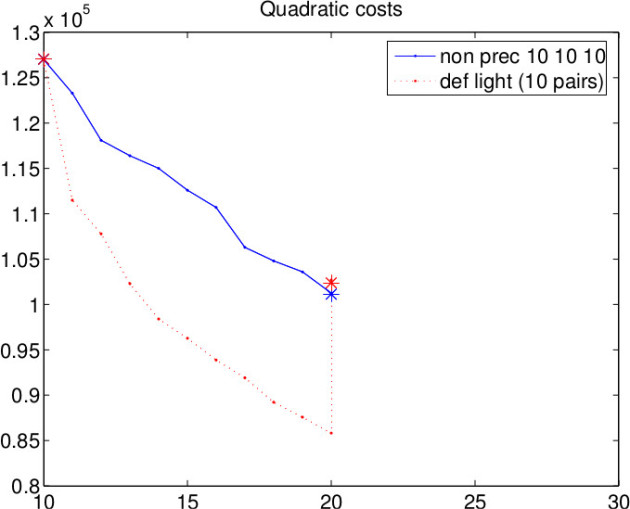
Something strange about deflation
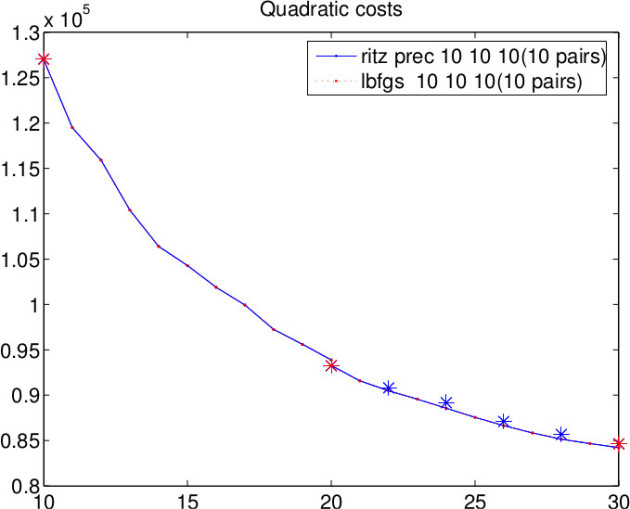
Ritz = L-BFGS for 10 pairs
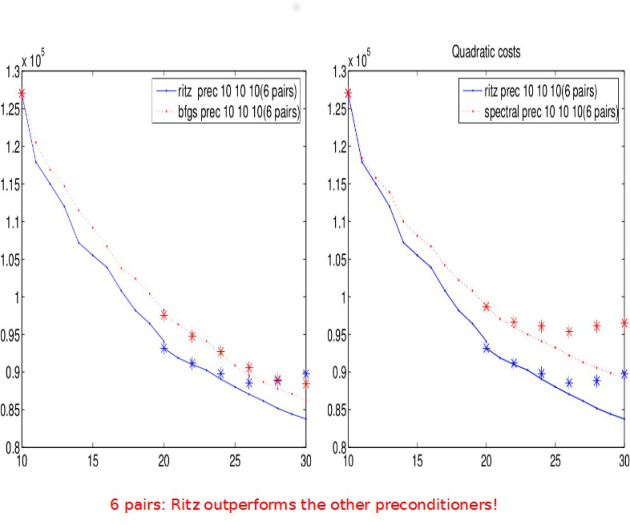
Preconditioner comparison
Comparison with the same number of pair (unfair, memory-wise spectral=bfgs cheaper than deflation=LBFGS)
Number of pair considered : 6 and 2
Remarks on our system !
Spectral preconditioner does not work in our case (
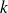vectors).L-BFGS/Ritz preconditioner: (
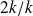)Based on by-products of CG.
More efficient than the spectral preconditioner or than no preconditioner.
Ritz is a stabilized version of spectral
Deflation: the computationally ”light” version is not efficient (
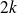).There is a ”full version” for all the preconditoners : work to prepare the preconditioner not neglectable, but robust wrt large matrix changes. The full form are being compared. They all have the same cost. Usefull when starting a system with poor initial guess. versions of the Ritz/Spectral/L-BFGS that do have the same property (and unfortunately cost). Usefull when starting a system with poor initial guess.
