Stopping criterion for data assimilation
CG truncation
Solving
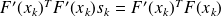(denoted
)
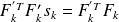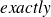is very expensive for large systems.For
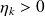, stop the CG method when
i.e. the stopping criterion is satisfied.
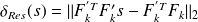
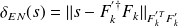(see "[Strakos, Tichy, 2005],[Arioli, 2004]"
)
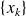converges locally to
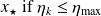and
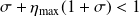
Why
? :CG converges monotonically in the energy norm.
Case of noisy problems.
Energy norm of the error for linear least-squares problems
Linear case
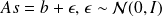(or after linearization,
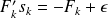)Maximum Likelihood estimate :
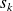minimizing
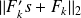
Backward error problem
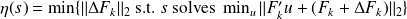
Closed solution
Want to have
below the noise level
.-
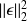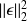follows a
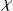squared distribution, with
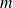dof.
Numerical experiment with the energy norm
Linear case
,
,
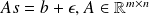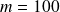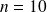
Two test-cases best discrete least-squares approximation of a function
as linear combination of
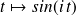(Well-cond. case),as linear combination of
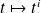(Ill-cond. case),
where the
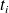's are equally spaced between in
, the exact solution being
.
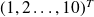is a Gaussian random vector
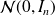. We plot the residual
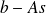for each CG iterate
and compute
The probability that a sample of
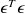is below
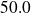is very weak (
).
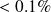Well-conditioned problem
Conditioned problem
Conclusion
Stopping criterion based on the energy norm of the error.
Natural when CG is used.
Interesting properties for noisy problems.
More test needed ...
