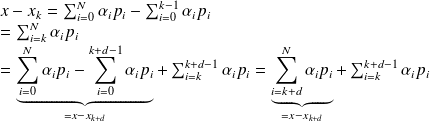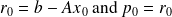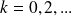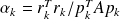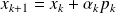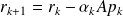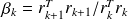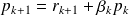The SPD case
The conjugate gradient method
The Ritz-Galerkin approach
The condition
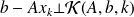can be written
.
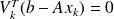Using
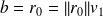we have
.
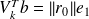Because
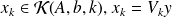and
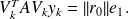
Note that
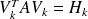is a by product of the algorithm.If
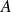is symmetric,
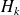reduces to a tridiagonal
.
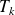Fundamental : Proposition 3
Because
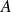is SPD, the bilinear form
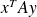defines an inner product.
The Ritz-Galerkin condition
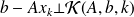can be written
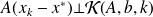which also reads
.
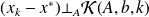This latter condition implies that
is minimal over
The Lanczos algorithm
In the Ritz-Galerkin approach the new residual
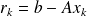is orthogonal to
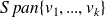such that
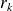is colinear to
.
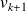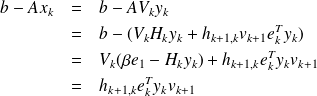
Since from
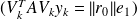
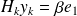. We can relax the normalisation constraints on the
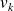such that
.
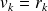Because
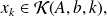there exists a polynomial
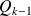of degree
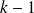such that
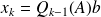
It follows that
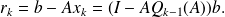From the
column of
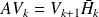we have
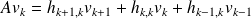
Using
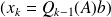in both sides of
and identifying the coefficient for b we obtain
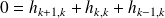which defines the scaling
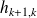enabling to have
Denoting
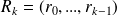we have
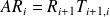, where
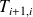is a tridiagonal matrix with entries
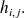
Similarly to the Arnoldi case we also have
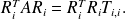
Because
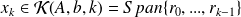, we have
.
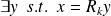The Ritz-Galerkin condition writes
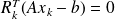, and hence
Using
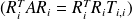we obtain
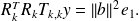
Because
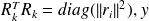is the solution of
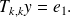
Note that for
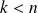the construction of the orthogonal basis mustterminate ; in that case
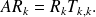
Let
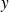be the solution of
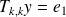then
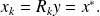Indeed,
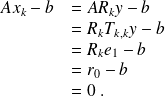
The main drawback of this approach is thet is requires to store
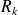to build
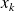from
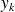. Notice that so far we have only use the symmetry property of
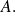Exploiting the positivness of
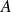leads to a clever variant of the above Lanczos algorithm that is better known as the Conjugate gradient method.
The CG Algorithm
|
Some properties of CG
An upper-bound for the convergence rate
From
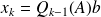
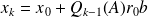we have that
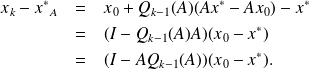
Then we have
. In addition,
is minimal over
.
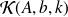Fundamental : Proposition 4
The polynomial
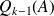built by CG is such that
,
where
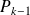is the set of polynomial of degree
.
Fundamental : Proposition 5
Let
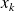be the
iterate generated by the CG algorithm then
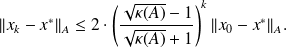
Proof
From Proposition (4) we have
.
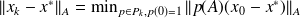Let
,
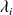be the eigenvalues of
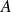and
where
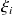
the components of
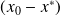in this eigenbasis
.
We have
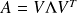, and
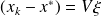then
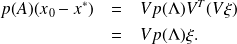
We therefore have that
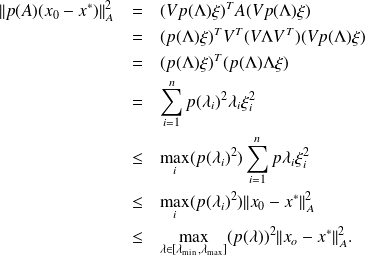
This shows that
Using an approximation theory result we have
where
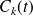is the Chebyshev polynomial of the first kind of degree
. For
we have
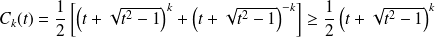
Let
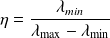we have
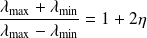
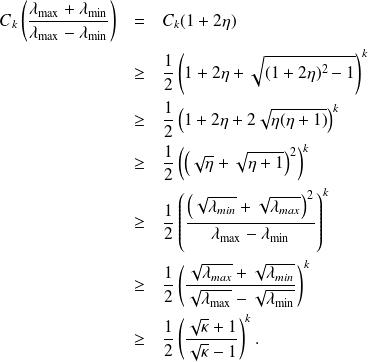
This implies that
.
Plugging this bound in
and then in
completes the proof.
Convergence v.s. the spectrum of A
For symmetric matrices, the degree of the minimal polynomial
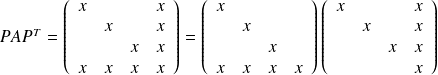
is equal to m the number of distinct eigenvalues.
Corollary 28
From Proposition(4) we have
.
This indicates that CG will converge in at most $m$ iterations for any initial guess
.
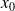Coollary 29
If
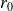has
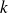components in the eigenbasis, CG will converge in
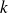iterations.
CG v.s. the A-norm of the error
Fundamental : Proposition 6
The CG iterates are such that
.
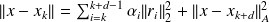he A-norm of the error is decreasing, if
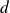is such that
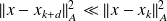
then
.
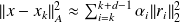Proof
In the CG algorithm, the vectors
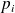are conjugate wrt to
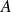. Remember
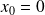. Let
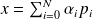be the solution
.
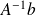The result follows easily from the Pythagore Theorem with inner product
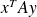on the expression
