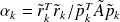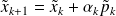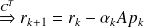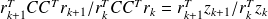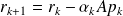Preconditioning
Why ”preconditionning” ?
The number of iterations of the Krylov solver is related to the spectrum of the matrix
:
The convergence is fast for matrices with few distinct eigenvalues in their spectrum.
For CG we have the well-known upper bound on the convergence rate
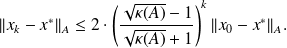
The closer
is from I, the faster the convergence.
solve an equivalent linear system that has a better eigenvalue distribution:
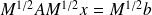with
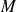symmetric and positive definite.
The preconditioner constraints
The preconditioner should
be cheap to generate and to store,
be cheap to apply,
ensure a fast convergence.
With a good preconditioner the computing time for preconditioned solution should be less than for the unpreconditioned one.
Preconditioned CG
The particular case of CG
For CG let
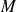be given in a factored form (i.e.
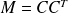), then CG can be applied to
with
,
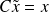and
.
Let define:
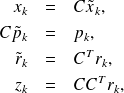
Note that
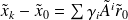writes
.
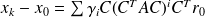Using
we can write the CG algorithm for both the preconditioned variables and the unpreconditioned ones.
| =
=
|
Writing the algorithm only using the unpreconditioned variables leads to :
|
Properties of PCG
A-norm minimization
The optimal property of CG (see Proposition 3) translates :
is minimal over
.
Notice, that
This shows that PCG also minimizes
but on a different space than CG.
A-orthogonality of the pk
That the vectors
form an A-conjugate set. This translates for
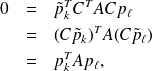
which shows that the
generated by PCG still form an A-conjugate set.
Orthogonality of the rk
By construction PCG builds a set of
that are orthogonal. For the
this translates for
which shows that the
generated by PCG are
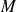-orthogonal.
Preconditioner taxonomy
There are two main classes of preconditioners
implicit preconditioners :
approximate
with a matrix
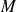such that solving the linear system
is easy.explicit preconditioners :
approximate
with a matrix
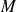and just perform
.Updating a preconditioner when multiple right-hand sides are given in sequenc
The governing ideas in the design of the preconditioners are very similar to those followed to define iterative stationary schemes. Consequently, all the stationnary methods can be used to defined preconditioners.
Lemma: First level preconditioning for Data assimilation
Fundamental :
Let
and
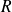be
matrices,
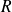being symmetric positive definite,
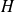be a
matrix and
. The following equality holds :
where
denotes the spectral condition number of the matrix
. Consequently, if we denote by
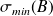is the smallest singular value of
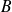
and if
, one has
.
On the opposite, if
, and
is the identity matrix, because
,
.
Proof of the Lemma
Let
be a singular vector associated with the smallest singular value of
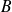noted
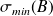. From the extremal property of the
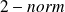follows
. Using the triangular inequality, and
yields
A similar calculation starting with
a singular vector associated with the largest singular value of
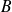shows that
Putting Inequalities
and
together, yields
for the preconditioned matrix, since the matrix
is semi-definite positive,
. From
we get that
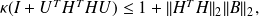
and that
The conclusion follows readily by replacing
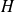by
in the previous inequality.
A sequence of linear least-squares problems
Originally developped for SPD linear systems with multiple right-hand sides (RHS).
Solve systems
,
with RHS in sequence, by iterative methods: Conjugate Gradient (CG) or variants.}Precondition the CG using information obtained when solving the previous system.
Extension of the idea to nonlinear process such as Gauss-Newton method. The matrix of the normal equations varies along the iterations.
The CG algorithm (A is spd and large !)
CG is an iterative method for solving
Iterations : Given
;
Set
Loop on
are residuals ;
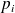are descent directions ;
are steps
The CG properties (in exact arithmetic !)
Orthogonality of the residuals:
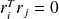if
of the directions:
if
The distance of the iterate
to the solution
is related to the condition number of
, denoted by
: 
-
The smaller
is, the faster the convergence. Exact solution found exactly in
iterations, where
is the number of distinct eigenvalues of
.
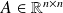The more clustered the eigenvalues are, the faster the convergence.
Why to precondition ?
Transform
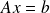in an equivalent system having a more favorable eigenvalues distribution.Use a preconditioning matrix
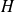(which must be cheap to apply).Ideas to design preconditioner
:-
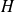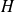approximates
.
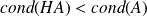
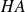has eigenvalues more clustered than those of
.
Note: when a preconditioning is used, residuals are :
Orthogonal if
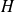is factored in
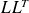.Conjugate w.r.t.
if
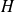is not factored.
