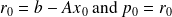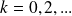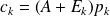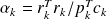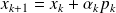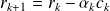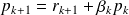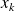The inexact CG for solving Ax = b
Inexact CG method
Take the basic CG method,
And perturb the matrix-vector products
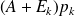
Easy way to control the inner {\em accuracy}.
Why ?
The matrix is not known with full accuracy (Parameter estimation, Schur complement,...)
Computing
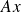with a poor accuracy is cheap (FMM)
The inexact CG Algorithm
|
Idea
Assume that
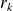goes to
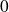
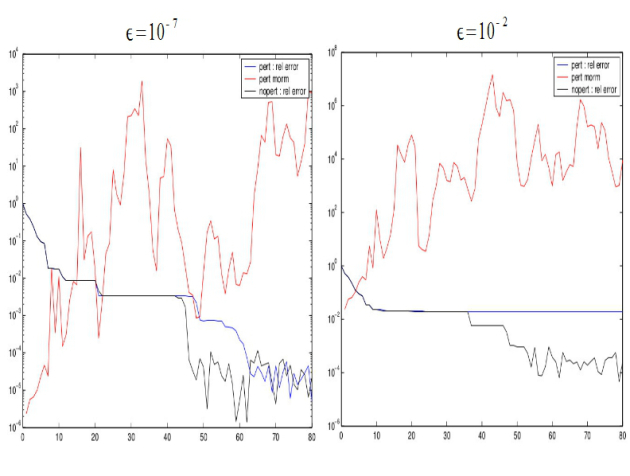
Control the residual gap
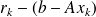by using
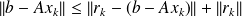
Note that for the exact algorithm,
is nonincreasing.Therefore, the norm chosen for the analysis is
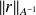for residual space, and the adjoint norm
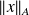for the solution space. To make this norm relative, we introduce the backward error
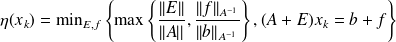
where
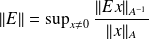.It is possible to show that
.
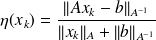The residual gap
Fundamental : Proposition 7
The residual gap in the inexact CG satisfies
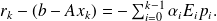
Proof
By an inductive argument. We have
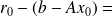0 and
.
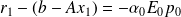Suppose the result true until step
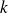. We have
.
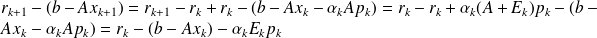Control of the residual gap(I)
Fundamental : Proposition 8
We consider the matrix norm
.
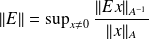Assume that
,
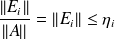The residual gap in the inexact CG satisfies
Proof
We have
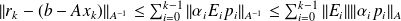, and
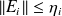concludes the proof.
Fundamental : A useful Lemma
Lemma 30
Let
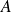be a symmetric and positive definite matrix. We consider the matrix norm
.
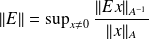For any symmetric matrix
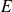, if
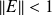holds, the matrix
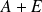is symmetric positive definite.
Proof
Assume that
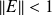. From the definition of the norm
we get
,
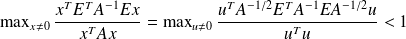which shows that
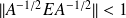, where
denotes the spectral norm.
Using
,
we get that
is symmetric and positive definite.
Using the Theorem of inertia of Sylvester yields that
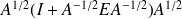is symmetric and positive definite, which is the desired result.
Control of the residual gap (II)
Fundamental : Proposition 9
Let
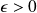and let
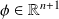be a positive vector such that
.
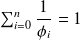If
,
we have that, for
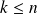
Proof
If
,
we have that
,
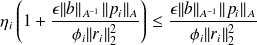which yields
.
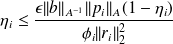Using
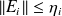, we get that
.
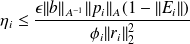Lemma (
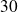)shows that
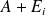is symmetric positive definite,
which implies that
.
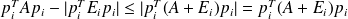In addition, we have
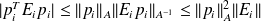, which yields
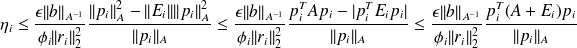
Taking into account that by definition we have that
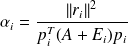, we obtain that
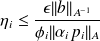. Using Proposition (
)gives
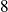Inexact CG : some results
