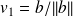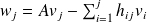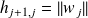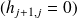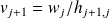Iterative solvers
Introduction
Alternative to direct solvers when memory and/or CPU constraints.
Two main approaches
Stationary/asymptotic method :
.Krylov method :
subject to some constraints/optimality conditions.
Advantages | Drawbacks |
|
|
|
|
Stopping criteria based on backward error analysis
The error introduced during the computation are interpreted in terms of perturbations of the initial data, and the computed solution is considered as exact for the perturbed problem. The backward error measures in fact the distance between the data of the initial problem and those of the perturbed problem. Let
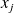be an approximation of the solution
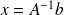. Then
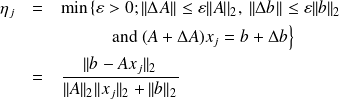
is called the normwise backward error associated with
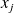. If perturbations are only considered on
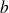or if
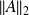is unknown
we can also consider
Notice that if
this reduces to a stopping criterion finds in many codes/papers.
Stationary methods
Basic scheme
Let
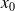be given and
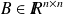a nonsingular matrix, compute
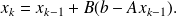
Note that
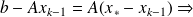the best
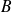is
.
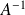Fundamental : Theorem
The stationary sheme defined by
converges to
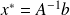for any
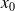if
, where
denotes the spectral radius of the iteration matrix
.
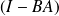Some well-known schemes
Depending on the choice of
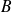we obtain some of the best known stationary methods.
Let decompose
, where
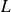is lower triangular part of
,
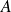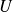the upper triangular part and
is the diagonal of
.
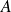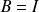: Richardson method,
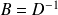: Jacobi method,
: Gauss-Seidel method.
Notice that
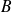has always a special structure and inverse must never been explicitely computed.
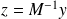reads solve the linear system
.
Krylov methods
Krylov methods: Motivations
For the sake of simplicity of exposure, we assume
.This does not mean a loss of generality, because the situation
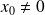can be transformed with a simple shift to the system for
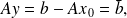
which obviously
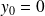. The minimal polynomial
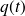of
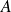is the unique monic polynomial of minimal degree such that
.
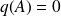It is constructed from the eigenvalues of
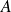as follows. If the distinct eigenvalues of
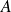are
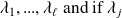has index $m_j$ (the size of the largest Jordan block associated with
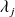), then the sum of all indices is
When
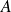is diagonalizable
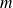is the number of distinct eigenvalues of
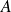; when
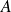is a Jordan block of size
, then
.
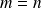If we write
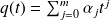, then
the constant term
.Therefore
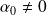if
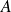is nonsingular. Furthermore, from
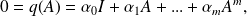
it follows that
.
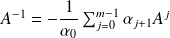This description of
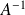portrays
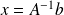immediately as a member of the Krylov space of dimension
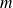associated with
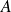and
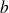denoted by
.
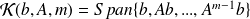The Krylov subspace approach
The Krylov methods for identifying
can be distinguished in four classes :
The Ritz-Galerkin approach :
construct
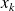such that
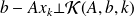.The minimum norm residual approach :
construct
such that
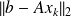is minimalThe Petrov-Galerkin approach :
construct
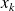such that
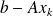is orthogonal to some other
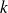-dimensional subspace.The minimum norm error approach :
construct
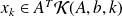such that
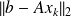is minimal.
Constructing a basis of K(A, b, k)
The obvious choice
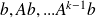is not very attractive from a numerical point of view since the vectors
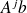becomes more and more colinear to the eigenvector associated with the dominant eigenvalue. In finite precision calculation, this leads to a lost of rank of this set of vectors.A better choice is to use the Arnoldi procedure.
The Arnoldi procedure
This procedure builds an orthonormal basis of
.
|
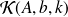The Arnoldi procedure properties
Fundamental : Proposition 1
If the Arnoldi procedure does not stop before the
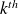step, the vectors
form an orthonormal basis of the Krylov subspace
.
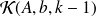Proof
The vectors are orthogonal by construction.
They span
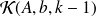follows from the fact that each vector
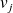is of the for
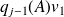, where
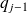is a polynomial of degree
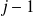. This can be shown by induction.
For
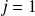is is true as
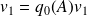with
.
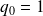Assume that is is true for all
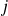and consider
.
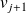We have
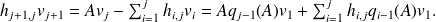
This shows that
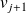can be expressed as
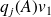where $
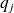is of degree
.
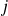Fundamental : Proposition 2
Denote
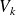the
matrix with column vector
;
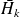the
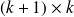Hessenberg matrix whose nonzero entries are
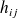and by
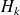the square matrix obtained from
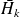by deleting its last row. Then the following relations hold :
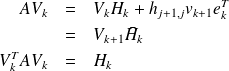
Proof
The relation
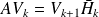follows from the equality which is derived from step 4, 5 and 7 of the Arnoldi's algorithm.
If we consider the
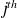column of
, i.e.
...
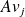This relation holds for all
. Relation
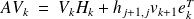is a matrix formulation of
.
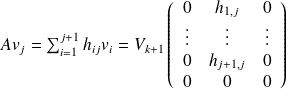It is derived from
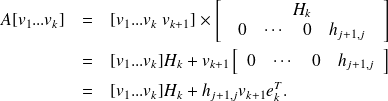
Relation
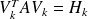mainly exploits the orthogonality of
.
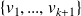