Intersection de deux sous espaces vectoriels
Fondamental : Théorème
Soient 
et 
deux sous espaces vectoriels de l'espace vectoriel 
. 
est un sous espace vectoriel de .
Exemple :
Soit 
l'ensemble des vecteurs 
.
Soient 
et 
.
et sont deux sous espaces vectoriels de 
et est l'intersection des ces sous espaces vectoriels.
est donc un sous espace vectoriel de .
Exemple : Contre exemples
Soient et deux sous espaces vectoriels de l'espace vectoriel .
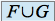n'est pas, en général, un sous espace vectoriel de 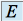. Le complémentaire dans
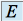de 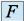n'est pas un sous espace vectoriel de .
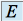