Définition et propriétés
Définition :
Soit
un
-espace vectoriel. 
est un sous espace vectoriel desur le corps si et seulement si est inclus dans, est non vide, etest un espace vectoriel pour les lois définies sur, mais restreintes à .
En principe , pour démontrer que est un sous espace vectoriel de E, il faut vérifier que 
et que les lois restreintes à possèdent les huit propriétés :
. En fait, il suffit de vérifier la stabilité des lois de composition.
Fondamental : Théorème
Soit un -espace vectoriel et 
. est un sous espace vectoriel de sur le corps si et seulement si :
-
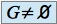
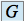- est stable pour les deux lois de compositions de 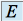, i.e. :
, on a : 
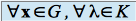, on a : 
