Application du déterminant
Fondamental : Théorème
Soit 
, la famille des 
vecteurs de 
, 
, formant les colonnes de 
est une base de si et seulement si : 
.
Reconnaître une famille libre
Méthode : Propriété
Soit 
un K-espace vectoriel de dimension , 
une famille de 
vecteurs de 
et 
, la matrice dont les colonnes sont les composantes des vecteurs dans une base quelconque de . La famille est libre si et seulement si on peut extraire de un déterminant d'ordre (appelé mineur d'ordre ) non nul.
Rang d'une matrice, d'une famille de vecteurs
Méthode : Propriété
Soit 
. 
(ou, de manière équivalente, le rang de la famille des 
vecteurs de
, formant les colonnes de est égal à ) si et seulement si :
il existe un mineur extrait de
d'ordre 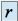non nultous les mineurs extraits de
d'ordre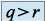 
sont nuls
Rang de la transposée d'une matrice
La propriété précédente nous permet d'énoncer :
Fondamental : Propriété
Soit . 
