Calcul pratique du déterminant d'une matrice de ℳn(K)
Méthode :
Il se fait par récurrence sur 
.
Tout d'abord, introduisons des sous matrices particulières de taille 
, extraites de la matrice 
dont on veut calculer le déterminant
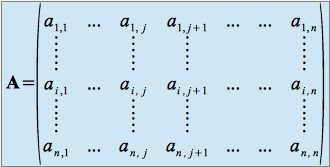
en enlevant la ligne 
et la colonne 
associées au terme 
dans la matrice 
, et que l'on notera 
. En utilisant ces notations, on a alors les résultats suivants :
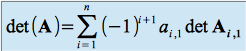par développement suivant la première colonne,
par développement suivant la première ligne.
Les deux développements précédents permettent de calculer par récurrence tout déterminant, en développant les déterminants des matrices d'ordre inférieur apparaissant dans ces développements, ceci jusqu'à l'ordre 1.
Ceci se généralise en développant suivant la colonne
,
ou bien encore en développant suivant la ligne
