1.3 Famille de courbes à vitesses bornées
On considère maintenant une famille de courbes à vitesses bornées que l'on choisit de paramétrer par ses intersections \(a\) avec l'axe \(t=0\). La courbe \({\cal L}_a\) passe donc par le point \((a,0)\) du plan \((x,t).\) L'ensemble des fonctions \(x_{{\cal L}_a}(t)\) qui décrivent les courbes \({\cal L}_a\) permet de définir une fonction \(X(a,t)\) à travers la relation \(x_{{\cal L}_a}(t) = X(a,t).\)
Définition :
On appelle \(X(a,t)\) le "mouvement 1D'' dont les trajectoires sont les courbes \({\cal L}_a\) dans le plan \((x,t).\) Il vérifie
\(x_{{\cal L}_a}(t) = X(a,t) \quad \hbox{et} \quad c_{{\cal L}_a}(t) =\left( \frac{d\, x}{dt}\right)_{\cal L} = \frac{\partial X }{\partial t}(a,t) .\) |
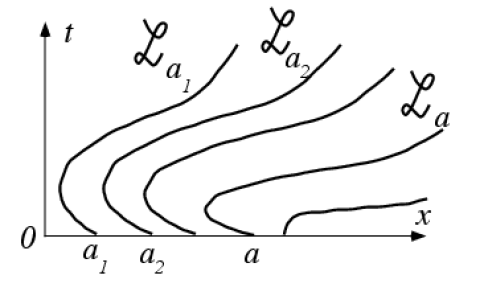
Lorsque les courbes \({\cal L}_a\) ne se coupent pas, il est possible de définir le mouvement inverse \(A(x,t)\) qui associe à tout point \(x\) la position \(a=A(x,t)\) à \(t=0\) de la courbe \({\cal L}\) qui passe par \(x\) au temps \(t.\)