Décomposition en modes propres
Même si le raisonnement s'applique à tous les systèmes décrit par la même équation, on prend ici l'exemple des petits déplacements d'une corde tendue de longueur \(L\) avec deux extrémités bloquées, qui vérifie l'équation des ondes \({\partial^2 y \over \partial t^2}(x,t) = c^2\; {\partial^2 y \over \partial x^2} (a,t)\) avec les conditions aux limites \(y(0,t)=y(L,t)=0\).
Définition : Modes propres d'oscillation
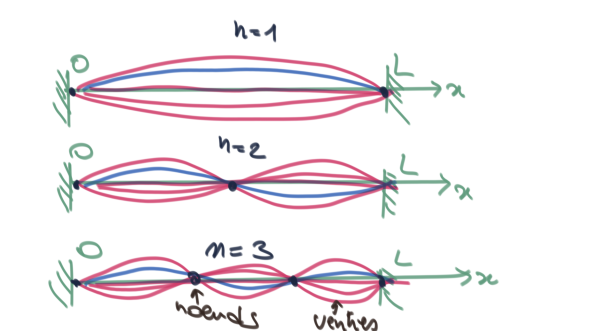
On appelle "modes propres" la suite de solutions \(y_n(x,t) = a_n \, \sin(k_n \, x) \, \cos(\omega_n\, t)\), avec \(k_n =n \, \pi /L\) et \(\omega_n = k_n \, c\) pour les valeurs entières \(n \in \mathbb N^*\). Il s'agit d'une famille de solutions stationnaires dont le nombre de noeuds et de ventre augmente avec \(n\). On montre que toute solution de l'équation des ondes avec les conditions aux limites considérées se décompose en une somme de modes propres :
Les modes propres forment donc une base dans l'espace des solutions du problème.