B(T) : potentiel de Mie et de Lennard Jones 12-6
Définition : Potentiel de paire : potentiel de Mie et de Lennard Jones 12-6
le potentiel de Mie s'exprime par :
![]()
et lorsque n = 12 et m = 6 on trouve le potentiel de Lennard Jones 12-6 :
![]()

On a ajouté au potentiel de sphère dure, purement répulsif, un terme attractif en 1 / rn.
Pour le potentiel de Lennard Jones, la forme mathématique en 1 / r6 représente à nouveau les interactions de type van der Waals. Mais comme on en a discuté dans le chapitre 2, d'autres contributions en 1 / r8 et en 1 / r10 existent et ne sont pas prises en compte ici.
Par rapport aux potentiels de Sutherland, de sphère dure et de puits carré, le terme répulsif est "adouci". Il décrit la répulsion dite "répulsion de Pauli" qui intervient aux faibles distances à cause du recouvrement des orbitales électroniques toutes chargées négativement.
Pour le potentiel de Lennard Jones, le choix de n = 12 est purement arbitraire et représente le carré de r6.
Second coefficient du viriel - Potentiel de Lennard Jones
L'intégration est complexe. Comme pour le potentiel de Sutherland, on peut exprimer l'exponentielle comme une série de Taylor puis intégrer par partie.
![]()
où la fonction gamma d'Euler vaut :
![]()
Remarque : variation avec la température
Comme pour le puits carré ou le potentiel de Sutherland, le second coefficient du viriel de Lennard Jones dépend de la température.
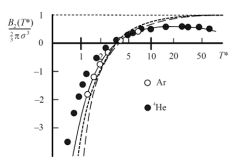
la ligne en trait plein sur la figure ci-dessus représente la variation de B(T) pour le potentiel de Lennard Jones.
C'est clairement le meilleur parmi les potentiels déjà décrit dans ce cours pour représenter les données expérimentales de l'argon ou de l'hélium.
A haute température, B(T) tends vers zéro ! et non pas vers le potentiel de sphère dure.





