B(T) : potentiel de Sutherland généralisé
Définition : Potentiel de paire : potentiel de Sutherland généralisé
le potentiel de Sutherland généralisé s'exprime par :
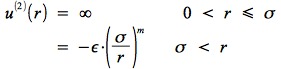

On a ajouté au potentiel de sphère dure, purement répulsif, un terme attractif en 1 / rm.
La forme mathématique en 1 / rm a une signification très particulière lorsqu'on la rapproche de la discussion dans le chapitre 2 sur les interactions de type coulombienne ou de type van der Waals, résumées dans le tableau ci-dessous :
En fait, Sutherland a proposé m = 6. Ce qui revient à modéliser les interactions attractives de van der Waals en 1 / r6 : (Cf chapitre 2)
les forces de polarisation existent entre les distributions de charges induites par les champs de polarisation. Dans le cas d'un dipôle mobile au voisinage d'une molécule non polaire. C'est le terme de Debye en 1/r6 de van der Waals.
les forces dipolaires : l'interaction entre deux molécules polaires proches est semblables à celle entre deux petits aimants caractérisés par des dipôles mobiles. C'est le terme de Keesom en 1/r6de van der Waals.
les forces de dispersion sont d'origine quantique et provoquées par des interactions entre dipôles induits et instantanés. Dites de "dispersion", ce sont elles qui assurent la cohésion ! Cette interaction est la contribution la plus importante des forces attractives, mêmes pour l'attraction entre molécules polaires. C'est le terme de London en 1/r6 de van der Waals.
Second coefficient du viriel - Potentiel de Sutherland
L'intégration est plus complexe. Néanmoins on peut exprimer l'exponentielle comme une série de Taylor puis intégrer par partie, ce qui donne une somme
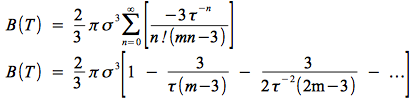
où
![]()
Remarque : variation avec la température
Comme pour le puits carré, le second coefficient du viriel de Sutherland généralisé dépend de la température.
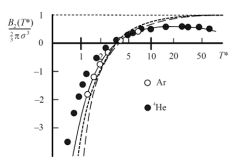
la ligne en petit pointillée sur la figure ci-dessus représente la variation de B(T) pour le potentiel de Sutherland avec m = 6.
Il a une forme analogue à celui du potentiel de puits carré.
A haute température, B(T) tends de nouveau vers la valeur obtenue pour le potentiel de sphère dure.






