Conséquence de B(T) sphère dure pour les équations d'état cubiques
Nous allons démontrer que les équations d'état cubique, l'une des plus importante classe d'équations d'état dans le monde industriel, contient un premier terme provenant d'un potentiel de sphère dure.
Démonstration
En tronquant au second ordre l'équation du viriel en pression,
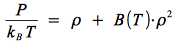, et en remplaçant le terme B(T) on obtient :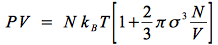
Ce qui indique que l'hypothèse de sphère dure provoque un accroissement de PV, par rapport au gaz parfait.
Réécrivons cette équation :
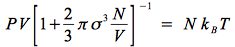
Or, nous pouvons faire une expansion binomiale
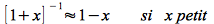puisque le terme x est le rapport du volume de la sphère dure sur le volume total. On obtient :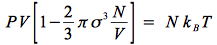
soit :
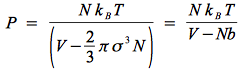
qui est le premier terme des équations d'état cubique.
Remarque : Ne pas restreindre l'équation d'état cubique au seul terme de sphère dure ! !
Il ne faut pas restreindre l'équation d'état cubique au seul terme de sphère dure ! En effet, nous venons de constater que le coefficient du viriel pour un potentiel de sphère dure n'a pas de dépendance avec la température, en totale contradiction avec l'expérience.
Heureusement les équations d'état cubiques contiennent un deuxième terme correctif, par exemple celle de van der Waals :
Voir aussi le chapitre 4.
