B(T) : potentiel de sphère dure
Définition : Potentiel de paire : potentiel de sphère dure (Hard Sphere)
le potentiel de sphère dure s'exprime par :
![]()
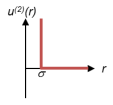
Modèle très simple → assimile les particules à des boules de billards de diamètre σ.
Mouvement libre et tout contact provoque répulsion (choc inélastique) ; ce qui arrive lorsque la distance entre deux centres de particules est égale à σ.
Potentiel très approximatif :
Les atomes ont une taille fixe, par exemple correspondant à la couche externe des électrons.
Cette couche externe est localisée dans un certain diamètre.s
faux d'après la mécanique quantique : la probabilité de localisation des électrons sur tout l'espace décroit avec l'éloignement du noyau atomique, mais n'est jamais nulle et donc s'étend à l'infini.
Ne tiens pas compte de l'interpénétration des nuages électroniques lorsque deux atomes s'approchent.
Que répulsif et aucune attraction.
(or les électrons négatifs d'un atome sont attirés par les noyaux positifs des autres atomes environnants).
Second coefficient du viriel - Sphère dure
L'intégration se fait entre 0 et σ puis entre σ et l'infini. On obtient facilement :
![]()
Remarque :
le second coefficient du viriel de sphère dure ne dépend pas de la température, ...ce qui est contraire aux observations expérimentales. Par exemple pour le méthane, B(T) croît avec la température selon la corrélation en cm3.mol-1 : B(T) = 42,5 – 16,75.10 3 / T – 25,05.10 5 / T² avec T en K. B(T) vaut -52 cm3/mol à 0°C et -33.3 cm3/mol à 50°C.

La figure ci-dessus indique la limite "sphère dure" (ordonnées réduite = 1), indépendante de la température. Or il existe une dépendance forte avec la température, comme le montrent les données expérimentales (ici argon et hélium) ou bien d'autres modèles (voir plus loin)
l'extension du potentiel de sphère dure à des mélanges, par exemple à des particules de taille différente σ1 et σ2 se fait par une règle de mélange classique : σmelange = 1/2 (σ1 + σ2





