Mean, Variance, and empirical estimators
Among quantities of interest we can introduce to feature the distribution, we can mention
the mean
the variance (or covariance matrix).
These quantities can be estimated from an ensemble of identical independent sample of the same random variable.
This also allows the estimation of the density distribution, called the empirical density.
Mean of random variable
By definition, the mean or expectation of a random variable X is defined as the integral
or from an ensemble of samples, by the limit of the empirical mean
when the number of sample increases toward infinity
Variance of random variable
The variance quatify the dispersion of the random variable around the mean. This is defined as
or from an ensemble of samples, by the limit of the empirical variance
The standard deviation
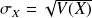has a more physical sens then the variance.
Covariance matrix
For random vectors, the equivalent of the variance is no more than the covariance matrix defined by
or from an ensemble of samples, by the limit of the empirical variance
Empirical distribution
The probability density function can be seen as the limit of the empirical probability density estimated from the samples
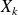
where
denotes the Dirac's distribution, when the number of samples increases to infinity
so that
