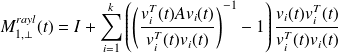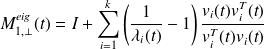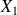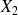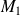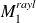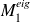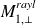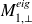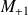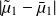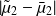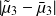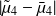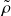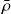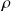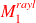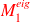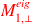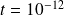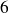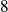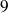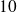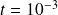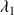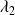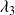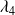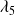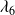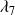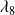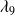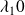Sensitivity of spectral preconditoners
Description of the preconditioners
Convergence of CG v.s. eigenvalues (I)
Role played by large and small eigenvalues in the convergence of CG not necessarily symmetric in practice.
Symmetry broken for many reasons : role of clusters, role of the right-hand side. Numerous experimental evidence
An analysis of the convergence in terms of eigenmodes reveals classes of problems where smallest eigenmodes are difficult to capture For instance, regularized least-squares, satisfying the discrete Picard assumption (Fourier coefficients of the RHS decay faster to 0 than singular values). In this case CG even used as a regularization tool ! [P.C. Hansen, SIAM 1998]
“Removing” the effect of small eigenvalues is often targeted
Mitigate the slowdown effect of the smallest eigenvalues (I)
Eigen-information
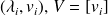 (small, approximated)
(small, approximated)Subspace deflation technique
Example,
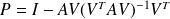 ,
,
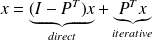 . Minimize the A-norm of the error on span(
. Minimize the A-norm of the error on span(
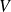 ) and solve for error equation iteratively [Frank, Vuik, 2001]
) and solve for error equation iteratively [Frank, Vuik, 2001]Or minimize the residual
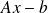 on
on
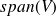 to get (
to get (
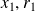 ) and minimize the residual
) and minimize the residual
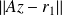 on a subspace orthogonal to
on a subspace orthogonal to
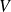 [Parks, de Sturler, Mackey, Johnson and Maiti, 2004]
[Parks, de Sturler, Mackey, Johnson and Maiti, 2004]
Note : comparable approaches used in a restarted framework to improve the convergence for small restarts [Bjorck, Grimme, van Dooren, 1994], [Morgan,1995,2000,2002], ...
Questions related to the use of approximate eigen-information
Question 1 : Study the role of the inaccuracy in the spectral elements on the ``quality'' of the spectral preconditionners
Question 2 : Is it possible to find criteria to screen the spectral information(keep only the relevant ones in the preconditioner)
Question 3 : The preconditioners involve quantities such as
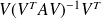 . For large systems computing
. For large systems computing
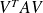 may be very expensive. What happens if we replace
may be very expensive. What happens if we replace
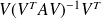 by
by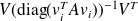 ( rayl. } approx.) or
( rayl. } approx.) or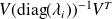 ( eig. approx.)
( eig. approx.)

Sensitivity analysis of spectral preconditioners
Sensitivity of the eigenvalues of the preconditioned matrix
Nonlinear perturbation of an eigenvalue problem
{Use first order perturbation theory: condition number approach
Consider the eigenelements as the eigenelements of a perturbed matrix
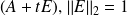 denoted by
denoted by
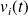 and
and
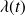 . This pairs are assumed to be simple so that first order expansions of
. This pairs are assumed to be simple so that first order expansions of
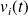 in
in
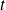 is available (recent overview in [Stewart, 2000]).
is available (recent overview in [Stewart, 2000]).Compute the first order expansion in
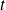 of the eigenvalues
of the eigenvalues
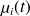 of the preconditioned matrix
of the preconditioned matrix
 .
.
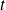 is an upper-bound of
is an upper-bound ofthe backward error
The preconditioners considered - Shift to one
The preconditioners considered - Shift to one (I)
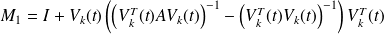 .
.In particular, this does not assume any scaling on the eigenvectors
For
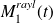 ,
,
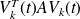 is replaced by
is replaced by
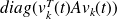
For
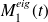 ,
,
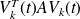 is replaced by
is replaced by
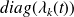
For
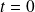 ,
,
 is a semi-simple eigenvalue of
is a semi-simple eigenvalue of
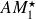 , with multiplicity
, with multiplicity
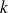 . (Perturbation theory for semi-simple eigenvalues needed {\color{violet} [Sun, 1990]}). Furthermore
. (Perturbation theory for semi-simple eigenvalues needed {\color{violet} [Sun, 1990]}). Furthermore
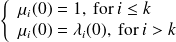
For
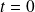 the traditional expression
the traditional expression
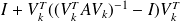 is recovered
is recovered
The preconditioners considered - Shift to one (II)
Using the orthogonality property of the eigenvectors, one may use
For
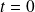 ,
,
 is a semi-simple eigenvalues of
is a semi-simple eigenvalues of
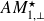 , with multiplicity
, with multiplicity
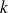 . (Perturbation theory for semi-simple eigenvalues again needed)
. (Perturbation theory for semi-simple eigenvalues again needed)
The preconditioners considered - Shift to one (III)
Coarse space preconditioners
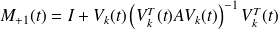
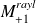 and
and
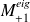 defined as previously}
defined as previously}
For
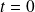 , the eigenvalues
, the eigenvalues
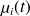 of
of
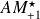 are simple in general,
are simple in general,
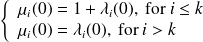
Theorem I : First order expansion
Fundamental :
The eigenvalues of the preconditioned matrices
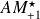 admit the first order expansions
admit the first order expansions
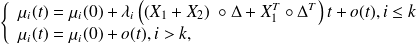
where
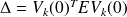 , and the
, and the
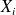 depend on the preconditioner. We can therefore define a condition number
depend on the preconditioner. We can therefore define a condition number
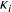 for the eigenvalue
for the eigenvalue
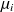 in the direction of
in the direction of
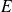 for
for
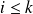 by [Rice, 66]
by [Rice, 66]
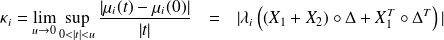
In addition,
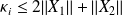 [Horn, Johnson, 1995]
[Horn, Johnson, 1995]
Matrices X1 and X2 for the various preconditioners
Define
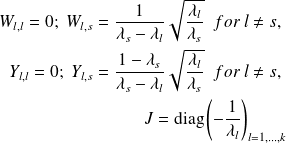
The entries of
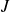 are large if some
are large if some
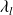 are small
are smallThe matrices
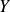 and
and
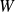 may have large entries if some
may have large entries if some
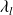 are clustered
are clustered
Prec |
|
| some cases of ill-conditioning |
| 0
| 0 0
| none cluster, small cluster, small |
|
| 0
| cluster, small cluster, small |
| 0 0 0 | 0 0
| none none small |
The terms “cluster” and “small” refer respectively to the presence of cluster or of small isolated eigenvalues.
Condition number and Backward Error
Backward error problem :
Let
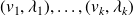 be approximate eigenpairs of
be approximate eigenpairs of
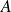 .
. The backward error associated is
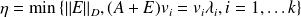
Using the same rule of thumb as for linear systems,
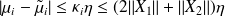
For the Frobenius norm,
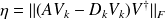 .This quantity is an upper-bound for the backward error in the spectral norm
.This quantity is an upper-bound for the backward error in the spectral norm This can be used to get an upper-bound on the forward-error in order to screen the eigen-information
Numerical illustrations
Difference between the computed and first order estimate
The eigenvalues of
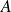 are
are
Precond |
|
|
|
|
| 3.8e-07 1.5e-06 2.3e-05 | 7.1e-08 1.5e-07 3.4e-07 | 2.8e-08 1.2e-06 3.5e-07 | 3.8e-08 3.8e-08 3.9e-08 |
| 1.4e-06 2.3e-05 | 8.1e-08 6.7e-07 | 9.6e-07 5.1e-07 | 3.8e-08 3.9e-08 |
| 5.7e-07 2.0e-06 2.2e-05 | 2.5e-07 3.0e-07 2.2e-07 | 3.9e-05 3.9e-05 1.2e-05 | 3.9e-05 4.0e-05 1.3e-05 |
The first order approximation accurately approximates the computed eigenvalues
Departure of the first order and approximate eigenvalues from 1
Numerical examples where the 3 smallest eigenvalues are targeted
Distance to one
The exact radius
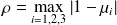
The computed radius
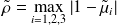
The estimated radius

Some clues to analyze the results
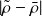 : validity of the first order approximation
: validity of the first order approximation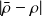 : asymptotic sensitivity
: asymptotic sensitivity
Case I: a small isolated eigenvalue
We take
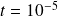 ,
,
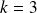 , the three smallest eigenvalues of
, the three smallest eigenvalues of
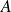 are
are
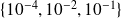 the
the
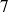 others are nicely located around
others are nicely located around
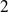 .
.
Precond |
|
|
|
| 3.7e-07 2.0e-03 1.8e-01 | 0.0e+00 2.0e-03 2.1e-01 | 0.0e+00 0.0e+00 0.0e+00 |
| 2.0e-03 1.8e-01 | 2.0e-03 2.1e-01 | 0.0e+00 0.0e+00 |
| 1.0e-01 1.0e-01 1.7e-01 | 1.0e-01 1.0e-01 2.1e-01 | 1.0e-01 1.0e-01 1.0e-01 |
Case II: a cluster of 3 eigenvalues around 1e-1
We take
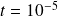 ,
,
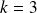 , the three smallest eigenvalues of $A$ are such that
, the three smallest eigenvalues of $A$ are such that
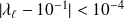 the 7 others are nicely located around
the 7 others are nicely located around
 .
.
Precond |
|
|
|
| 4.2e-10 2.5e-02 2.5e-02 | 0.0e+00 2.7e-02 2.7e-02 | 0.0e+00 0.0e+00 0.0e+00 |
| 2.3e-02 2.3e-02 | 2.4e-02 2.4e-02 | 0.0e+00 0.0e+00 |
| 1.0e-01 1.0e-01 1.0e-01 | 1.0e-01 1.0e-01 1.0e-01 | 1.0e-01 1.0e-01 1.0e-01 |
A more complicated example
Not really covered by our theory
{Matrix
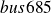 (Harwell-Boeing)
(Harwell-Boeing)Symmetrically preconditioned by Incomplete Cholesky factorization (threshold
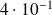 )
)The right-hand side
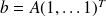
Stopping criterion : unpreconditioned residual norm reduced by
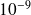 (
(
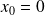 )
)We take
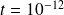 and
and
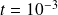 and report the number of PCG iterations to reach convergence when the number of eigenvectors
and report the number of PCG iterations to reach convergence when the number of eigenvectors
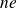 is varied
is varied
number of PCG iterations
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
All Prec | 161 | 147 | 132 | 118 | 106 | 95 | 88 | 81 | 81 | 79 |
| ||||||||||
|
|
|
|
|
|
|
|
|
|
|
| 168 168 168 | 154 155 156 | 142 152 154 | 129 142 141 | 122 144 143 | 114 139 140 | 107 133 134 | 104 131 194 | 101 126 183 | 98 121 183 |
| 168 168 | 155 156 | 151 152 | 139 140 | 138 139 | 133 133 | 125 125 | 124 184 | 121 173 | 117 171 |
| 168 168 168 | 154 155 156 | 142 152 152 | 129 139 140 | 121 138 139 | 114 133 133 | 107 125 125 | 104 124 184 | 101 121 174 | 98 117 171 |
The ten smallest eigenvalues of the IC preconditioned matrix
5.67e-04 |
2.91e-03 |
3.58e-03 |
4.71e-03 |
6.19e-03 |
8.35e-03 |
1.85e-02 |
2.05e-02 |
3.04e-02 |
3.05e-02 |
Concluding remarks
The sensitivity of a set of spectral preconditioners studied
Approximations in the preconditioners may results in poor performance, as observed numerically
Comparison of spectral preconditioners has to take into account their sensitivity to inexact eigen-infomation
Implemented in the CERFACS ocean data assimilation system
Study the unsymmetric case ...